Um jovem casal deseja ter dois filhos. Analisando as condições do casal, o médico afirma que a probabilidade deles terem dois meninos é de 40% e que a chance do primeiro bebê a nascer ser menina é 50%. O médico também informou que se o primeiro filho for menina, a probabilidade condicional do segundo ser menina é de 40%. Denotem as variáveis aleatórias por , se o bebê for menino e , se o bebê for menina no i-ésimo nascimento . Encontre:
- A distribuição de probabilidade conjunta de e com suas distribuições de probabilidades marginais.
- A probabilidade do segundo filho do casal também ser um menino, dado que o primeiro foi um menino.
- A covariância entre e .
Passo 1
(a)
Vamos considerar assim.
Denotando 0 pra menino e 1 pra menina, e só podem assumir esses dois valores, 0 ou 1.
O que o problema quer é que a gente monte nossa tabelinha.
Passo 2
Primeiro vamos organizar as informações pra nossa tabela, de acordo com o enunciado.
A prob. de os dois serem meninos é de 0,4, então:
Prob. da primeira ser menina é 0,5:
A última informação é:
De cara a gente já pode pensar que se a prob. do primeiro ser menina é 0,5, então a prob. do primeiro ser menino é 0,5 também, concorda?
Passo 3
Com a última informação do encunciado mais a fórmula da prob. condicional, a gente sabe que:
Já sabendo que .
Com isso a nossa tabela fica a princípio assim.
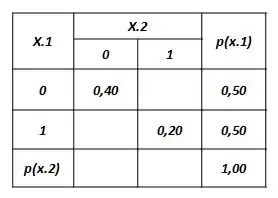
Passo 4
Vamos completar a tabela, bem tranquilo né? Só lembrar que a soma dos valores do interior da tabela tem que dar igual ao valor da distribuição marginal.
Exemplo:
A tabela completa ficaria assim.
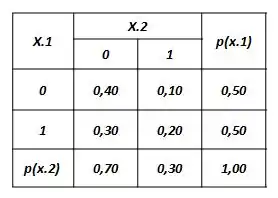
Passo 5
(b)
Prob. condicional que o exercício pede é .
Aplicando a fórmula.
É só pegar todos os valores da tabela.
Da distribuição marginal de .
E:
Substituindo na fórmula.
Passo 6
(c)
Temos que calcular .
Pela fórmula,
Vamos calcular cada parcela aí.
Passo 7
Pra calcular e é só multiplicar cada valor possível dessas variáveis pelas suas respectivas probabilidades né ? Que ficam na distribuição marginal.
Já:
Lembrou ? Multiplica os valores possíveis das variáveis pelos valores de dentro da tabela.
Passo 8
Substituindo na fórmula da covariância.