Sejam e variáveis aleatórias discretas com a seguinte função de probabilidade conjunta:
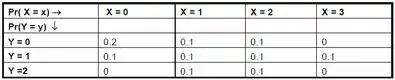
Pede-se:
Calcular a covariância de e , , e o coeficiente de correlação detalhando seus passos para a obtenção de cada termo.
Passo 1
Bom, estamos trabalhando com um problema em que as nossas variáveis aleatórias são discretas, o que implica em possuir um conjunto finito de resultados, e além disto, este é um problema de probabilidade conjunta.
Probabilidade conjunta ocorre quando pelo menos 2 variáveis aleatórias afetam o problema. Como pode ser percebido no caso da questão, estamos trabalhando com as variáveis e .
Antes de passarmos para o objetivo da questão, que é calcular a covariância de e , e depois calcular o coeficiente de correlação (mais adiante será deixado claro o motivo deste coeficiente ser calculado apenas depois), precisamos determinar dois parâmetros que a questão nos deu: as distribuições marginais e .
A ideia por trás da distribuição marginal é simples. Lembra que estamos com uma distribuição conjunta ? Então, imagina aí: o que aconteceria se a gente fixasse um determinado e variasse o ? Se somarmos todas essas probabilidades, obteríamos uma probabilidade deste nosso evento acontecer.
Pronto, esta é uma ideia resumida da distribuição marginal. Mas sim, o que importa é como calcular. E como fazemos isto? Aí já é mais fácil ainda! É só nós somarmos as linhas (colocando o resultado final na última coluna a direita) e somarmos as colunas (colocando o resultado final na última linha abaixo).
Por fim, é basicamente acrescentar uma linha e uma coluna a tabela dada na questão. Portanto, temos:
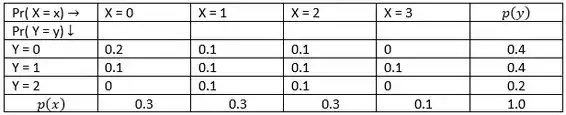
Passo 2
Agora, vamos para a parte de cálculos em si! Começaremos pela covariância, ou seja, de uma forma simples, seria a média do produto dos desvios das nossas variáveis e .
Mas o que importa mesmo é como calcular a covariância? E aí? Como fazer?
Para isto, podemos aplicar a seguinte relação:
Mas o que seriam estas funções e ? Elas são as esperanças (a mesma ideia de uma média). Para calcularmos as esperanças, podemos utilizar as seguintes relações:
Conseguem ver o motivo de termos obtido as distribuições marginais? Para calcularmos e precisamos das probabilidades e . Então, nós nos adiantamos no problema!
Agora, vamos calcular primeiramente as esperanças e . Portanto,
Simples. Para calcular , pegamos o valor de cada e multiplicamos pelo seu respectivo e depois somamos todos os termos. E o mesmo ocorreu para .
Agora, vamos calcular . É importante tomarmos cuidado pois temos um somatório dentro do somatório. A ideia é trabalhar do somatório de dentro para o de fora. Então, vamos começar a expandir estes somatórios:
Agora, vamos analisar o valor de cada separadamente (seria o respectivo a cada linha da nossa tabela). Para , temos:
Já para , temos:
Por fim, para , temos:
Portanto, a esperança é:
E agora podemos finalmente calcular a nossa covariância que é dada por:
Passo 3
Agora, podemos partir para o cálculo do coeficiente de correlação . No passo 1 foi dito que ele só poderia ser calculado depois da covariância. E isto decorre de um simples motivo, basta olhar a fórmula deste coeficiente:
Agora fica claro né? O coeficiente de correlação é função da covariância! E como já calculamos este termo, só nos falta as variâncias de cada variável aleatória e .
Relembrando, calculamos as variâncias através das seguintes relações:
Portanto, agora é só expandirmos as nossas séries com os valores corretos de cada um dos elementos. Relembrando, , e a nossa tabela:
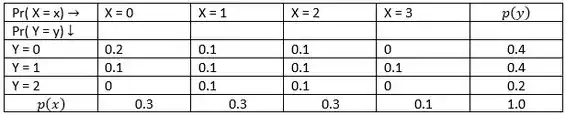
Portanto, começando pela variância de , temos:
Já para a variância de , temos:
Por fim, basta substituirmos todos estes valores na fórmula do coeficiente de correlação. Ele é dado então por: