Duas roletas idênticas, que podem resultar nos números e com igual probabilidade, serão colocadas para rodar simultaneamente. Nesse contexto, defina as seguintes variáveis:
Menor número observado entre os resultados das duas roletas.
Maior número observado entre os resultados das duas roletas.
- Construa a tabela da função de probabilidade conjunta de e .
- Obtenha a distribuição condicional de dado .
- Calcule a variância de .
Passo 1
Tá, a gente vai rodar as duas roletas, vamos primeiro observar quais seriam as possíveis combinações de resultados delas.
Foi? resultados possíveis.
A tabela que a gente tem que montar é uma assim:
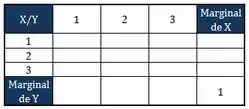
Lembrando que:
Passo 2
Tá, vamos preencher isso aí. Os valores de dentro da tabela, cruzando as linhas com as colunas, são as interseções entre e , certo?
Então, a primeira coisa que eu queria que você notasse é que tipo, cruzando por exemplo a linha com a coluna , eu estaria procurando a probabilidade do menor número observado ter sido e o maior observado ter sido ... isso é possível? Oo
Não né? Não dá pra o maior resultado ser e o menor ser se .
A gente consegue concluir então que todas as interseções onde são impossíveis, certo? E assim a probabilidade será zero.
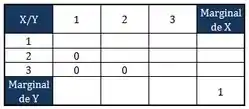
Passo 3
Agora vamos calcular as outras probabilidades de interseções:
Concorda? O único resultado favorável é o que aí o menor resultado e o maior resultado são .
Resultados favoráveis seriam: e .
Resultados favoráveis seriam: e .
Resultado favorável: .
Resultados favoráveis: e .
Resultado favorável: .
Lembrando que pra obter as marginais é só fazer a soma das linhas e colunas, tranquilo... fica assim a tabela:
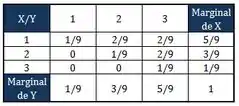
Passo 4
(b)
A gente tem que calcular a condicional:
Mas vamos ter três possibilidades né?
Pra todas elas é tranquilo, é só dividir o valor da interseção (que é cruzar as linhas com as colunas) pelo valor da probabilidade total de , que tá na marginal de .
Passo 5
Assim, a gente tem:
É isso aí!
Passo 6
(c)
Temos que calcular . Existe uma fórmula pra isso, que é:
Lembrando que:
Agora só calcular tudo, só conta, mas muita conta.
Passo 7
Passo 8
Agora junta tudo:
Resposta