PUCRIO - (Cálculo 2 - MAT1162) - G1 (Versão C) 2020.1
Considere os vetores
- Determine a área do paralelogramo formado pelos vetores e
- Determine o ângulo formado entre os vetores e
- Verifique se os vetores , e são coplanares, ou seja, pertencem ao mesmo plano
Passo 1
Fala galera, tudo certinho? Olha, pra início de conversa, vamos dar uma boa olhada nesses três vetores.
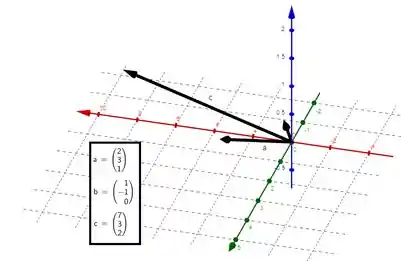
Agora, a primeira coisa que a questão pede é a área do paralelogramo definido por e . Oras galera, isso nada mais é do que o módulo do produto vetorial deles. Sendo assim, temos:
Calculando a determinante, temos:
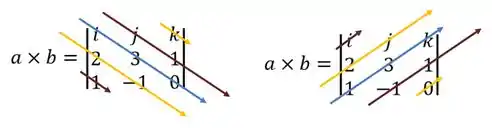
E calculando o módulo desse vetor, achamos:
Passo 2
Show galera, vamos pra próxima letra. A próxima letra pede pra gente o ângulo formado entre e . Oras, pra isso, basta a gente lembrar que, pela regra do produto vetorial, podemos tirar ainda que:
Bem, uma coisa de cada vez. A começar por esse numerador. Esse produto será:
Aplicando a distributiva, temos:
Agora pros módulos dos vetores, temos que:
De forma que o produto fica:
Feshow galera! Juntando denominador e numerador, achamos:
Pra achar o ângulo basta usar a trigonométrica inversa correspondente!
Passo 3
Galera, ultima letra. Ó só, detalhe importante: se eu pegar dois vetores só, eles vão sempre ser coplanares. Então já sabemos que são, mas será que o está contido no plano que formam? Pra isso, vamos olhar esse resultado da letra :
Povo, o produto vetorial sempre dá um vetor, e esse vetor resultante é perpendicular ao plano definido por . Pô, então se for coplanar, ele terá que ser também perpendicular ao vetor ! Como vetores perpendiculares tem produto escalar nulo, basta calcularmos:
E vamos achar:
No final das contas não é que são coplanares mesmo!
Resposta
- são coplanares