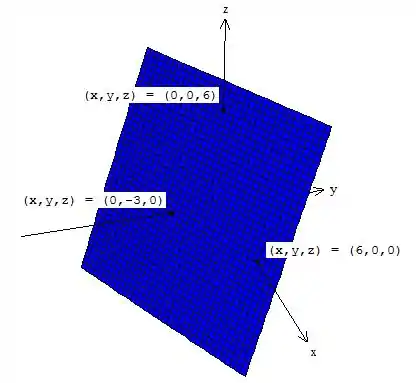
Encontre a equação do plano que passa por e é perpendicular ao vetor da origem até , e esboce seu gráfico.
Passo 1
Para encontrar a equação do plano, precisamos de dois elementos:
- Um ponto pertencente ao plano.
- E um vetor normal ao plano
O problema já fornece diretamente um ponto pertencente ao plano .
Passo 2
Agora, temos de encontrar o vetor normal ao plano. Porém, podemos achá-lo calculando o vetor , que é o vetor que vai da origem até .
Calculando :
Passo 3
Agora basta encontrar a equação do plano:
Passo 4
Vamos fazer os traços do plano.
- Traço no plano :
- Traço no plano :
- Traço no plano :
O eixo é interceptado no ponto e o eixo também tem um ponto de
interseção em
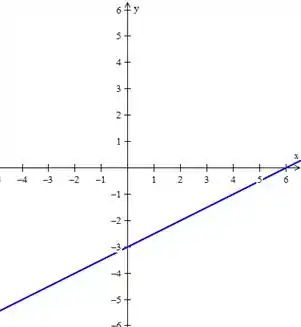
O eixo é interceptado no ponto e o eixo também tem um ponto de interseção em
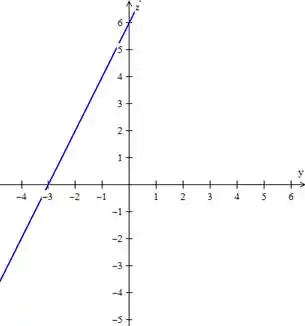
O eixo é interceptado no ponto e o eixo também tem um ponto de interseção em
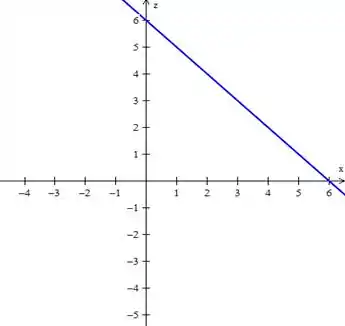
Passo 5
Marcando os pontos , fazendo o paralelogramo, hachurando sua área, o gráfico fica:
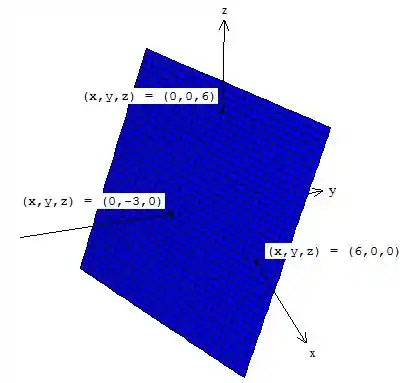
Resposta
A equação do plano é:
E o seu esboço: