USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 5 - Curvas no R3, Superfícies de Nível, Questão 1.4d
1.4. Verifique quais das curvas abaixo estão contidas na superfície . Verifique a sua resposta plotando, em algum software, a superfície e a curva num mesmo gráfico.
d.
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema queremos saber se a curva dada por
Está contida na superfície .
Sabe como verificamos isso? 🤔
O segredo é substituir em e verificar se a equação formada possui solução.
Por exemplo, a superfície é dada pela equação
Já a curva é dada genericamente por
Assim reescrevendo como
Sacou a ideia? 😉
Passo 2
No nosso caso, a partir de , temos
Substituindo na superfície ...
Nesse caso a igualdade não foi satisfeita, logo não é solução de e, portanto, não está contida na superfície.
Se plotarmos e vamos ver
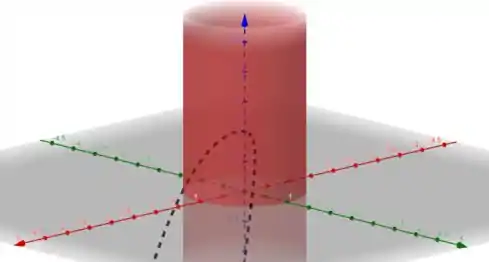
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
Não está contida.