Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação do Plano

Ver Teoria
Exercício 13123456789101112141516171819

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 5 - Curvas no R3, Superfícies de Nível, Questão 1.3c

1.3. Verifique quais das curvas abaixo estão contidas na superfície S : x 2 + y 2 - z 2 = 0 . Verifique a sua resposta plotando, em algum software, a superfície e a curva num mesmo gráfico.

c. α t = t , 1 2 - t 2 2 , 1 2 + t 2 2 ,     t ∈ R

Passo 1

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema queremos saber se a curva α t dada por

α t = t , 1 2 - t 2 2 , 1 2 + t 2 2 ,     t ∈ R

Está contida na superfície S : x 2 + y 2 - z 2 = 0 .

Sabe como verificamos isso? 🤔

O segredo é substituir α t em S e verificar se a equação formada possui solução.

Por exemplo, a superfície S é dada pela equação

x 2 + y 2 - z 2 = 0

Já a curva α t é dada genericamente por

α t = x t , y t , z t

Assim reescrevendo S como

x t 2 + y t 2 - z t 2 = 0

Sacou a ideia? 😉

Passo 2

No nosso caso, a partir de α t , temos

x t = t y t = 1 2 - t 2 2 z t = 1 2 + t 2 2

Substituindo na superfície S ...

x 2 + y 2 - z 2 = 0 → x t 2 + y t 2 - z t 2 = 0

t 2 + 1 2 - t 2 2 2 - 1 2 + t 2 2 2 = 0

Simplificando a equação

t 2 + 1 4 - t 2 2 + t 4 4 - 1 4 + t 2 2 + t 4 4 = 0

t 2 + 1 4 - t 2 2 + t 4 4 - 1 4 - t 2 2 - t 4 4 = 0

Eliminando os temos opostos...

t 2 - t 2 2 - t 2 2 = 0

t 2 - t 2 = 0

0 = 0

Portando α t é solução de S , logo está contida na superfície...

Plotando S e �� t , temos

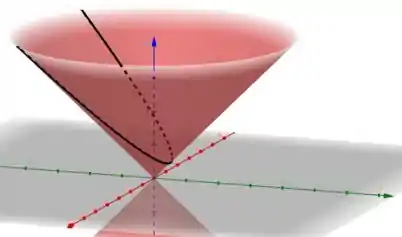
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

Está contida.

Exercícios de Livros Relacionados

Coloque a equação na forma padrão, classifique a superfície e esboce-a. y 2 = x 2 + 1 9 z 2
Determine uma equação da superfície constituída de todos os pontos P para os quais a distância de P ao eixo x é o dobro da distância de P ao plano y z . Identifique a superfície.
Nos exercícios 1 a 6 , esboce o gráfico da superfície de equação dada. 2 x + y + 5 z - 1 0 = 0 .
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. 16 x 2 = y 2 + 4 z 2
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. x 2 + 4 z 2 - y = 0