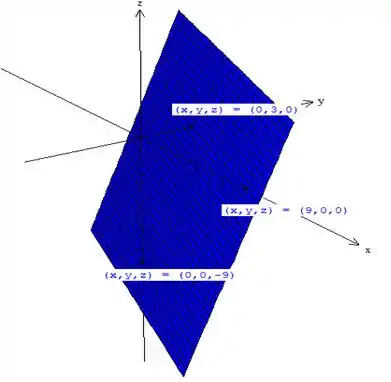
Encontre a equação do plano que passa por , e e esboce seu gráfico.
Passo 1
Para encontrar a equação do plano precisamos do vetor normal e de um ponto pertencente ao plano. Beleza?
O problema nos fornece 3 pontos pertencentes ao plano. Ou seja, só nos falta encontrar o vetor normal
Vamos começar encontrando vetores pertencentes ao plano.
Passo 2
Temos dois vetores pertencentes ao plano: e
Se fizermos o produto vetorial entre eles, teremos um vetor que é simultaneamente ortogonal a : e , e consequentemente normal ao plano. Então temos:
Passo 3
Pronto!!! Temos um vetor normal ao plano. Agora é só montar a equação do plano. Mas qual ponto eu escolho para utilizar como ponto pertencente ao plano na equação??? Qualquer um. Tanto faz. Vou escolher o ponto . Temos:
Passo 4
Vamos fazer os traços do plano.
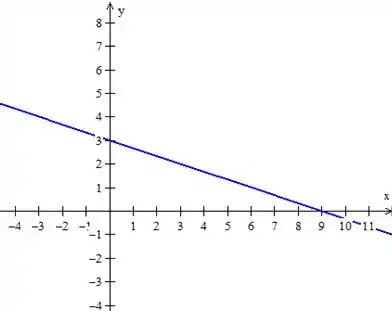
- Traço no plano :
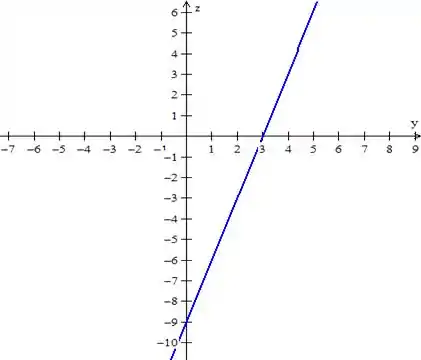
- Traço no plano :
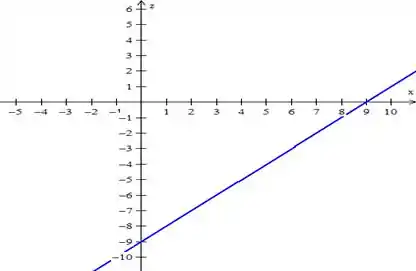
- Traço no plano :
O eixo é interceptado no ponto e o eixo também tem um ponto de
interseção em
O eixo é interceptado no ponto e o eixo também tem um ponto de interseção em
O eixo é interceptado no ponto e o eixo também tem um ponto de interseção em
Passo 5
Marcando os pontos , fazendo o paralelogramo, hachurando sua área, o gráfico fica:
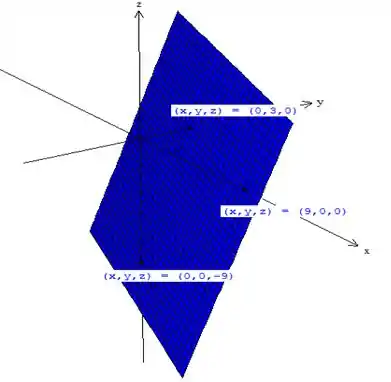
Resposta
A equação do plano é:
E o seu esboço: