Uma barra uniforme de comprimento e de massa desprezível é suspensa horizontalmente por uma dobradiça e uma corda, conforme a figura abaixo. Um bloco de peso é colocado sobre a barra de forma que a dobradiça fique a uma distância do seu centro, como mostrado na figura. Se a tensão da corda não pode exceder , quais são o máximo valor de e o módulo da força sobre a dobradiça nesta situação?
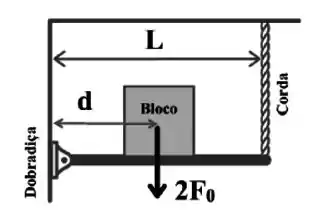
Passo 1
Para resolver esse exercício, temos que lembra de um conceito lá na parte de tensão em Física. A gente sabe que a tensão é uma força exercida por uma corda, fio ou um objeto similar em um ou mais objetos. Qualquer coisa pendurada, puxada ou suspensa por uma corda está sujeita a uma tensão.
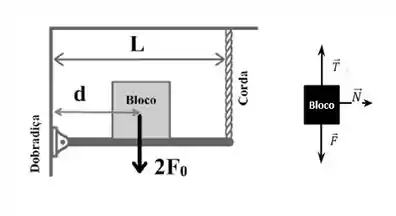
No nosso sistema, a condição para que o bloco não se mova exige que e para que permaneça em equilíbrio estático. O enunciado nos diz que o máximo valor de para que haja equilíbrio é quando a tensão, sobre a corda é .

Passo 2
Escolhendo como referência o eixo de rotação que passa pela dobradiça de forma perpendicular ao plano da figura, tem-se que
,
Portanto, resolvendo a igualdade temos:
Passo 3
Sendo a força sobre a dobradiça, e sabendo que a força peso que age no bloco é igual a temos que:
onde é a tração máxima na corda
portanto
Resposta
Letra a