Júlia foi contratada para ajudar a pintar a fachada de um prédio, mas não está convencida da segurança do equipamento. Uma prancha de 5,0 m é suspensa horizontalmente, do topo do prédio, por cordas presas a cada extremidade. Júlia sabe, de experiência anterior, que as cordas utilizadas se romperão se a tração exceder a 1,0 kN. Seu chefe, de 80 kg, desconsidera as preocupações de Júlia e começa a pintar, quando está a 1,0 m de uma extremidade da prancha. Se a massa de Júlia é 60 kg e a massa da prancha é 20 kg, qual é a região que Júlia pode ocupar sobre a prancha, para ajudar seu chefe, sem provocar o rompimento das cordas?
Passo 1
Vamos tentar entender o que está acontecendo no problema.
Temos duas forças de tração nas extremidades, o peso da prancha no centro de gravidade, o chefe a 1,0 metro de uma das extremidades, e uma distância x que Júlia pode ocupar.
A figura abaixo retrata isso:
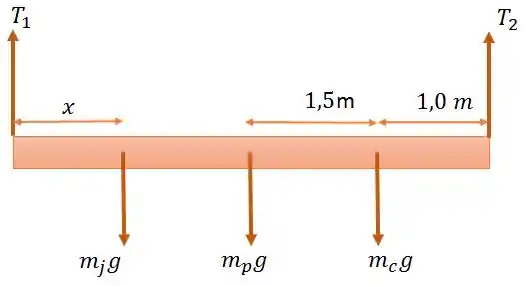
Passo 2
Como a prancha está em equilíbrio, podemo aplicar a condição de torque resultante igual a zero para relacionar x com as outras distâncias e forças.
Então:
Escolhendo o eixo da esquerda como eixo de rotação, montamos a seguinte equação:
Substituindo os valores
Colocamos o valor máximo de tração, para sabermos o valor máximo de x.
Resolvendo a equação:
Como com a tração se rompe, Júlia deve ocupar o espaço de