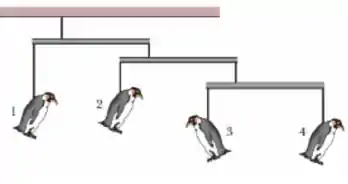
A figura mostra um móbile de pinguins de brinquedo pendurados em um teto. As barras transversais são horizontais, têm massa desprezível e o comprimento à direita do fio de sustentação é três vezes maior do que o comprimento à esquerda do fio. O pinguim tem massa . As massas dos pinguins , e são respectivamente:
(a) , ,
(b) , ,
(c) , ,
(d) , ,
(e) , ,
Passo 1
Cada uma dessas barras transversais está em equilíbrio. Se olharmos pra barra que tem os pinguins e
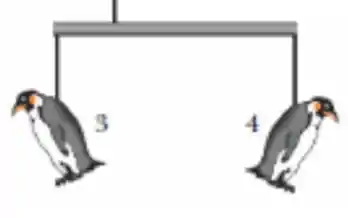
Temos que a condição de equilíbrio é que o somatório dos torques seja nulo. Tomando como positivo um torque que faça a barra rotacionar no sentido horário, temos
O enunciado diz que o comprimento a direita é 3 vezes o comprimento a esquerda. Se chamarmos a distância a esquerda de e o da direita de , vamos ter que
Passo 2
Agora vamos pegar a barra do meio
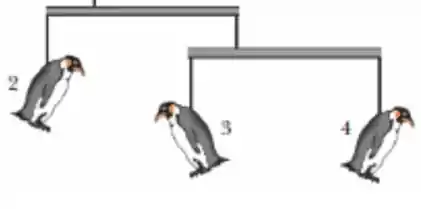
Do lado esquerdo temos a massa do pinguim 2 e do lado direito temos as massas dos pinguins 3 e 4. Assim
Passo 3
Agora na última barra temos o pingüim 1 na esquerda e na direita os pinguins , e . Assim
A nossa opção é a letra B!
Resposta
(b)