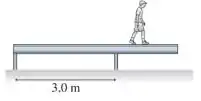
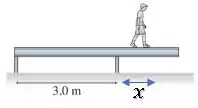
Uma viga homogênea de e de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na figura abaixo, distantes uma da outra. Um garoto de começa a caminhar ao longo da viga. Quanto ele pode se afastar da extremidade esquerda da viga sem que ela tombe?
(A)O garoto pode se afastar uma distância de da extremidade esquerda da viga.
(B) O garoto pode se afastar uma distância de da extremidade esquerda da viga.
(C) O garoto pode se afastar uma distância de da extremidade esquerda da viga.
(D)O garoto pode se afastar uma distância de da extremidade esquerda da viga.
(E) O garoto é capaz de alcançar a extremidade direita da viga sem que ela tombe.
Passo 1
A viga inicialmente está apoiada nas duas pilastras.
Mas se o garoto começa a andar muito para o lado direito, talvez a viga comece a...

Tombaaaaaaaar, ahhhh...
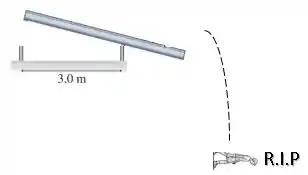
Nãoooo podemos deixar que isso aconteça, né.
Então, vamos calcular direitinho qual a distância que o garoto pode se afastar sem que a viga tombe.
Mas como calculamos isso?
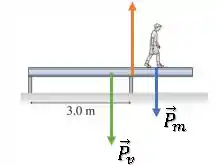
Quando o menino está bem antes da posição que faz a viga tombar, temos duas forças normais sustentando o conjunto, uma em cada pilastra:
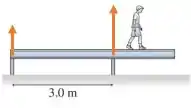
A medida que o menino anda para a direita, o força normal do pilar da esquerda vai diminuindo e diminuindo até uma situação limite onde ela é nula:
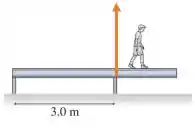
Nesse instante, todo o conjunto está apoiado pela pilastra da direita.
Mas porque essa viga está equilibrada nesse ponto?
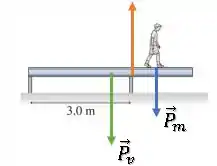
Isso acontece porque as forças peso do menino e da viga (cada uma de um lado) geram um torques que se anulam com relação ao ponto da pilastra da direita:
Se o menino andar um pouquinho a mais para a direita essa viga tomba, porque o torque de seu peso será maior que o torque do peso da viga , logo a barra entra em rotação no sentido horário.
Então, vamos calcular a posição do menino que faz esses torques estarem em equilíbrio, assim, achamos a posição limite que o menino pode chegar.
Passo 2
Então, como a barra está em equilíbrio, temos que o torque resultante será nulo.
Vamos calcular o torque resultante com relação ao ponto apoiado da viga:
O torque resultante será a soma dos torques de cada força:
Passo 3
O torque da força normal é nulo, pois essa força está aplicada no próprio ponto de rotação:
Passo 4
O torques das forças peso não são nulos.
Eles serão dados pelo produto vetorial entre o vetor e o vetor força :
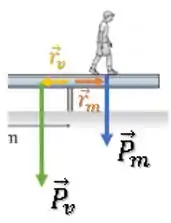
Como os vetores são perpendiculares aos vetores , o módulo desses torques serão dados por:
Passo 5
O módulo dos torques será:
Mas cada força tenta fazer a viga girar em um sentido diferente, portanto, esses torques terão sinais opostos.
Vamos considerar o torque que faz a viga girar no sentido horário positivo, por livre e espontânea vontade mesmo hahah.
O peso da viga está aplicado ao centro de massa da viga, que se econtra no seu centro.
Então, a distância dessa força à pilastra da direita é:
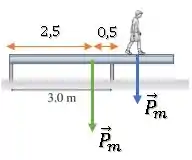
Então o torque do peso da viga será:
O sinal é negativo seguindo nossa conveção de sentido (horário).
Enquanto o torque do peso do menino será:
O sinal é positivo seguindo nossa conveção de sentido (anti-horário).
Como não sabemos a distância ainda, chamaremos de :
Passo 6
Agora, vamos à equação do torque resultante de novo:
Passo 7
Como a distância do menino à pilastra da direita é , sua distância à extremidade esquerda será:
Ficamos com a letra (D).
Resposta
Letra (D)