O sistema abaixo consiste em uma barra de massa desprezível pivotada na posição indicada pela letra d. As posições indicadas pelas letras de a até f estão espaçadas igualmente. Assinale falso ou verdadeiro às afirmações abaixo. Neste item não é necessário justificativa.
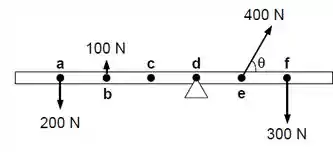
O sistema ficará em equilíbrio se a resultante das forças à esquerda e à direita do pivô forem iguais;
O sistema ficará em equilíbrio quando for igual ;
O sistema ficará em equilíbrio quando for igual ;
O sistema ficará em equilíbrio se e uma força de for aplicada na vertical para cima em c;
O sistema ficará em equilíbrio se e uma força de for aplicada na vertical para baixo em c;
Passo 1
Vamos observar uma afirmação de cada vez.
“O sistema ficará em equilíbrio se a resultante das forças à esquerda e à direita do pivô forem iguais”
FALSO
A condição de equilíbrio é que:
Então se a resultante das forças forem iguais, nós garantimos que seu somatório seria zero, mas não o dos torques, visto que eles dependem da distância das forças até o pivô.
(Para termos um equilíbrio estático, também seria necessário que , mas não vamos considerar isso nessa questão.)
Passo 2
“O sistema ficará em equilíbrio quando for igual ”
VERDADEIRO
“O sistema ficará em equilíbrio quando for igual ”
FALSO
O torque que a força em gera é devido à sua componente vertical.
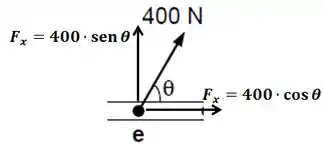
Se considerarmos que o espaçamento entre cada ponto é , e como todas as forças fazem com a posição do ponto onde atua ( em relação a barra), o somatório dos torques fica:
Para observarmos os sinais, podemos ou usar a regra da mão direita, ou perceber que as forças e (nos pontos e ) causam uma rotação no sentido horário, enquanto e (nos pontos e ) causam uma rotação no sentido anti-horário.
Se , temos , e teremos:
Logo, temos equilíbrio.
Se , temos , e teremos:
Logo, não temos equilíbrio.
Passo 3
“O sistema ficará em equilíbrio se e uma força de for aplicada na vertical para cima em c”
VERDADEIRO
“O sistema ficará em equilíbrio se e uma força de for aplicada na vertical para baixo em c;”
VERDADEIRO
Vamos usar o somatório dos torques do passo anterior.
Se , temos e logo:
Logo, ainda não temos um equilíbrio. Mas se uma força de for aplicada na vertical para cima em , ela faria um torque:
Que é exatamente o que precisávamos! Agora sim:
No segundo caso temos , .
Ao adicionar a força de na vertical para baixo em :
Resposta
O sistema ficará em equilíbrio se a resultante das forças à esquerda e à direita do pivô forem iguais;
O sistema ficará em equilíbrio quando for igual ;
O sistema ficará em equilíbrio quando for igual ;
O sistema ficará em equilíbrio se e uma força de for aplicada na vertical para cima em c;
O sistema ficará em equilíbrio se e uma força de for aplicada na vertical para baixo em c;