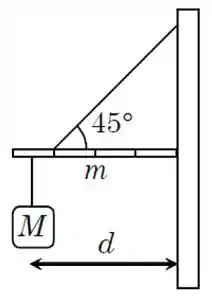
Uma haste horizontal de e de comprimento está apoiada contra a parede sem atrito. Uma corda fazendo um ângulo de com a direção vertical mantêm a haste em equilíbrio estático. O ponto de amarração fica a uma distância de da parede. A que distância da parede deve ser pendurada uma massa para manter o equilíbrio?
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiro temos que apontar as forças sobre essa haste!
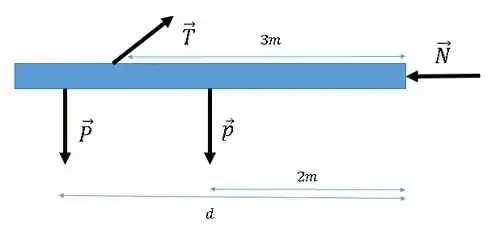
Onde é o peso da haste, é o peso da massa , é a tração do fio e é a normal entre a haste e a parede.
Passo 2
Agora temos que definir qual será o eixo de rotação. Pensa aqui comigo: se não houvesse essa massa a haste ia continuar presa na corda e a sua extremidade direita iria descer! Assim o nosso eixo de rotação é no ponto onde a corda tá amarrada.
Com a tensão da corda e a normal atuam na direção do eixo de rotação, essas duas forças não exercem torque. Assim o nosso torque resultante é devido ao peso da massa e o peso da haste.
Tomando como positivo torque que faz rotações no sentido horário, temos que
Como o sistema está em equilíbrio
O peso da massa atua a uma distância do eixo de rotação enquanto que o peso do centro de massa da haste está a um metro desse eixo
Assim a nossa opção é a letra A
Resposta
(a)