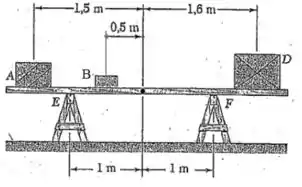
Três caixas são colocadas em uma prancha de madeira uniforme de que está apoiada em 2 cavaletes, equidistantes do cento da prancha, conforme indicado na figura ao lado. As massas das caixas são e , respectivamente. A respeito da massa do bloco A assinale a alternativa correta.
a) O valor mínimo da massa do bloco é e o sistema está na iminência de girar no sentido horário
b) O valor mínimo da massa do bloco é e o sistema está na iminência de girar para no sentido horário
c) O valor máximo da massa do bloco é e o sistema está na iminência de no sentido horário
d) O valor máximo da massa do bloco é e o sistema está na iminência de girar no sentido anti-horário
e) Não é possível determinar a massa do bloco com as informações fornecidas.
Passo 1
O valor mínimo da massa de é tal que faz com que a normal em , , seja nulo:
Isso acontece porque o sistema está na iminência de girar no sentido horário. Colocando o referencial de giro( o pivô) em , podemos chegar na equação do equilíbrio de torques .
Assim:
Isolando
Passo 2
O valor máximo é descoberto fazendo-se a normal no ponto nula, . Nessa situação, o sistema está na iminência de girar no sentido horário.
Escolhendo o ponto de giração em ( o pivô) teremos:
Assim, a letra c) é a correta.
Resposta
c)