Uma viga de comprimento é carregada por três homens, um em uma das extremidades e os outros dois segurando a viga com uma barra transversal posicionada de tal forma que a carga da viga é dividida igualmente entre os três homens. A que distância da extremidade livre está a barra de apoio? (Despreze a massa da barra de apoio).
a) ;
b) ;
c) ;
d) ;
e) ;
Passo 1
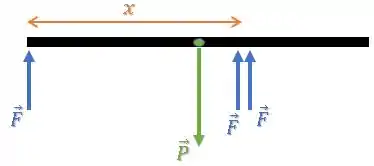
A barra está sendo carregada por três homens.
Se o peso da barra está igualmente distribuído, isso significa que todos os homens realizam uma força de mesmo módulo que chamaremos de .
Um deles segura a barra pela extremidade e os outros dois estão a uma certa distância do primeiro:
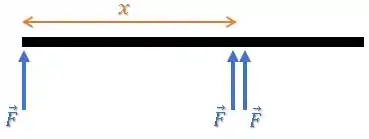
Bom, mas e o peso da barra?
Consideramos que o peso da barra está aplicado sobre seu centro de gravidade (CG).
Como a barra é uniforme, esse CG estará em seu centro.
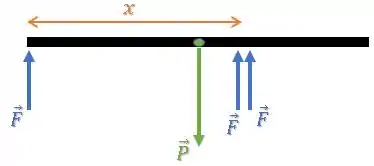
Okay, entendi o que está acontecendo...
Mas como é que achamos essa tal de distância ??
Bom, podemos usar as condições de equilíbrio:
Passo 2
Se utilizarmos a equação de somatório de forças, conseguimos descobrir a relação entre a força e a força peso , o que será útil depois.
Mas estamos mais interessados na distância , então vamos utilizar a equação do somatório de torques (envolve distância).
Passo 3
Próxima coisa a fazer é escolher um ponto para o cálculo do torque.
Aqui a gente tem a liberdade de escolher qualquer ponto da barra. Uma boa sugestão é a extremidade onde está aplicada.
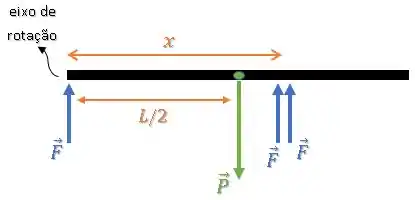
Passo 4
Agora, vamos aplicar o somatório de torques é igual a zero.
Vamos assumir sentido horário positivo e o sentido anti-horário negativo, mas isso também é uma escolha.
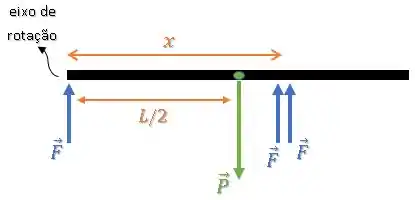
Lembrando que o torque da força que está aplicada sobre o eixo de rotação é nulo, então sobra:
Passo 5
Temos, agora, que relacionar as forças e para encontrar a distância apenas em função do comprimento da barra .
Para isso, vamos utilizar a primeira condição de equilíbrio... somátorio de forças igual a zero.
Passo 6
Substituindo essa relação em , temos:
Mas muuuuuuuuuuita atenção!!!!
Essa ainda não é nossa resposta.
Nós queremos saber a distância da barra de apoio a partir da extremidade livre da barra, ou seja, o outro lado...
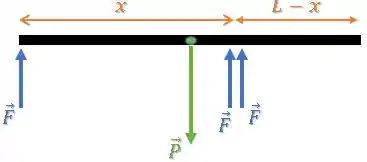
Ficamos com a letra A.
Resposta
Letra (A)