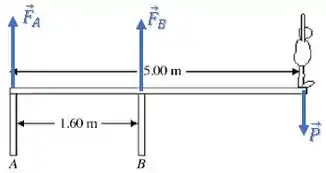
Um mergulhador cuja massa é de encontra-se no extremo de uma prancha de de comprimento e com massa desprezível. A prancha é mantida em equilíbrio graças a dois pilares separados de , como mostrado na figura, que podem exercer forças verticais, para baixo ou para cima, dependendo da situação. As intensidades e os sentidos das forças exercidas pelos pilares A e B sobre a prancha na situação mostrada abaixo são, respectivamente
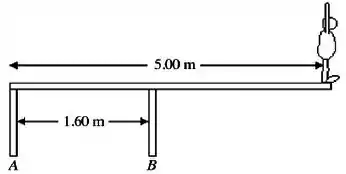
Dados:
(A) para baixo e para cima.
(B) para baixo e para baixo.
(C) para cima e para cima.
(D) para cima e para baixo.
(E) para cima e para baixo.
Passo 1
Nesse problema, temos uma força conhecida do peso do mergulhador:
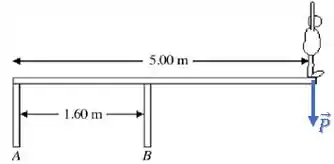
E também duas forças desconhecidas em A e B, digamos que para cima:
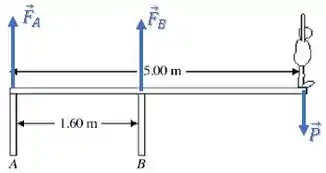
Para que a prancha esteja em equilíbrio, temos que tanto a força quanto o torque resultante é nulo:
Passo 2
Vamos começar com a equação de equilíbrio de torques.
Podemos escolher qualquer ponto para calcular o torque a partir dele.
Mas facilita a nossa vida escolher um ponto onde alguma força desconhecida está sendo aplicada. Isso porque o torque dessa força com relação ao ponto de aplicação é nulo, facilitando nossas contas.
Vamos escolher o ponto A, por exemplo.
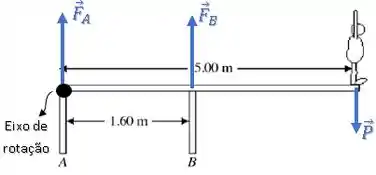
Considerando o sentido horário positivo, temos:
Agora já conhecemos uma das forças.
Passo 3
Para achar a outra força, poderíamos aplicar novamente a equação equilíbrio de torques mudando o eixo de rotação de lugar...
Ou então, simplesmente usar a outra condição, equilíbrio de forças.
Opaaaa, achamos um valor negativo!
Lembra que nós chutamos o sentido das forças e lá no início?
Então, como achamos um valor positivo para , nosso chute foi certo para o sentido dessa força.
Porém, como achamos um valor negativo para , nosso chute inicial foi errado e na verdade essa força aponta no sentido contrário (para baixo):
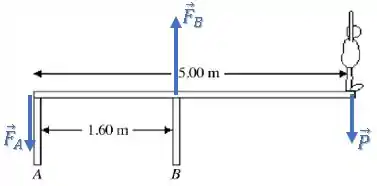
Então, nossas forças são:
Ficamos com a letra (A).
Resposta
Letra (A)