Um mergulhador com 580 N de peso está em pé na extremidade de um trampolim de comprimento e massa desprezível (figura abaixo).
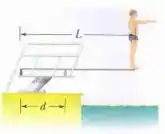
O trampolim está preso em dois suportes separados por uma distância . Das forças que agem sobre o trampolim, quais são
- O módulo da força exercida pelo suporte de trás.
- O sentido (para cima ou para baixo) da força exercida pelo suporte de trás.
- O módulo da força exercida pelo suporte da frente.
- O sentido (para cima ou para baixo) da força exercida pelo suporte da frente.
Passo 1
Para descobrir o módulo da força exercida pelo suporte de trás, vamos usar o suporte da frente do ponto de rotação.
A distância da força exercida pelo suporte de trás até o ponto de rotação é .
A distância do ponto de atuação do peso do mergulhador até o ponto de rotação é
.
Sendo a força do suporte de trás e usando a condição de equilíbrio. Percebemos que como a força peso tende a girar no sentido horário, podemos dizer que o suporte de trás tende a girar no sentido anti-horário.
Passo 2
b) Para descobrirmos o sinal da força, basta analisarmos a figura.
A força peso tende a girar no sentido horário e o suporte de trás no sentido anti-horário. Para que isso ocorra a força do suporte de trás tem que ser negativa, ou seja, para baixo.
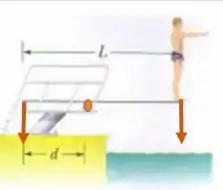
Passo 3
c) Para analisar a força do suporte da frente, vamos colocar o ponto de rotação no suporte de trás.
A distância da força exercida pelo suporte da frente até o ponto de rotação é .
A distância do ponto de atuação do peso do mergulhador até o ponto de rotação é
Sendo a força do suporte da frente e usando a condição de equilíbrio. Percebemos que como a força peso tende a girar no sentido horário, podemos dizer que o suporte da frente tende a girar no sentido anti-horário.
Poderíamos também ter feito
O resultado seria o mesmo!
Passo 4
d) Para descobrirmos o sinal da força, basta analisarmos a figura.
A força peso tende a girar no sentido horário e o suporte da frente no sentido anti-horário. Para que isso ocorra a força do suporte da frente tem que ser positiva, ou seja, para cima.
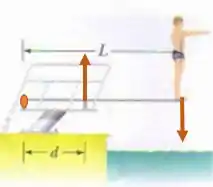
Resposta
- 1160N
- Para baixo
- 1740N
- Para cima