Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Escoamento Laminar e Turbulento e Perda de Carga

Ver Teoria
Exercício 81234567910111213141516171819

Enunciado

Uma compressão constante sobre o pistão na Figura produz uma vazão Q = 0,15   c m 3 / s através da agulha. O fluido tem ρ = 900   k g / m 3 e μ = 0,002   k g / ( m ∙ s ) . Qual a força F   necessária para manter o escoamento?

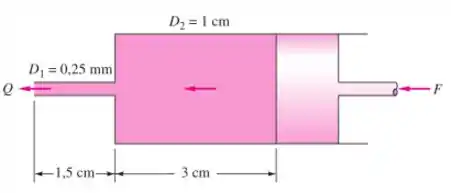
Passo 1

Então galera, mais uma vez aplicaremos a equação da energia e veremos o que nos falta para resolver o problema:

p 1 ρ g + V 1 ² 2 g + z 1 + h p = p 2 ρ g + V 2 ² 2 g + z 2

Neste caso a perda de carga fica do lado 1, pois é a “saída” do escoamento.

Podemos dizer que não há variação na altura dos cilíndros, logo z 1 = z 2 :

p 1 ρ g + V 1 ² 2 g = p 2 ρ g + V 2 ² 2 g + h p

Pela expressão Q = V A podemos encontrar quanto valem nossa velocidades em cada parte do escoamento:

V 1 = Q π D 1 ² 4

Passando Q e D 1 para o Sistema Internacional:

Q = 0,15 c m 3 s = 0,15 × 10 - 6 m 3 s

D 1 = 0,25   m m = 0,25 × 10 - 3   m

Substituindo na equação:

V 1 = Q π D 1 ² 4

V 1 = 0,15 × 10 - 6 π 0,25 × 10 - 3 ² 4

V 1 = 4 π 0,15 0,0625 10 - 6 10 - 6

V 1 = 9,6 π   m / s ≅ 3,06   m / s

Fazendo o mesmo para V 2 :

D 2 = 1   c m = 1 × 10 - 2   m

V 2 = Q π D 2 ² 4

V 2 = 0,15 × 10 - 6 π 1 × 10 - 2 ² 4

V 2 = 4 × 0,15 π 10 - 6 10 - 4

V 2 = 4 × 0,15 π 10 - 2

V 2 = 0,006 π ≅ 0,0019   m / s

Como V 2 ≪ V 1 , vamos supor que V 2 ≈ 0 , ficamos com a equação:

p 1 ρ g + V 1 ² 2 g + h p = p 2 ρ g

Passo 2

Calcularemos agora a perda de carga h p representada pela perda de carga no tubo menor 1 mais o a do tubo maior 2:

h p = f 1 L 1 D 1 V 1 ² 2 g + f 2 L 2 D 2 V 2 ² 2 g

Como V 2 = 0 :

h p = f 1 L 1 D 1 V 1 ² 2 g + 0

Verificamos se podemos usar o fator de atrito laminar:

R e d = ρ V 1 D 1 μ = 900 × 3,06 × 0,25 × 10 - 3 0,002 = 344,25 < 2300

Verificada a condição de laminaridade:

f 1 = 64 R e d = 64 ρ V 1 D 1 μ

Logo:

h p = 64 ρ V 1 D 1 μ L 1 D 1 V 1 ² 2 g

h p = 32 L 1 V 1 μ ρ g D 1 ²

Antes de substituirmos valores, vamos levar a expressão da energia:

p 1 ρ g + V 1 ² 2 g + h p = p 2 ρ g

Reescrevendo:

p 1 - p 2 ρ g = - V 1 2 2 g + 32 L 1 V 1 μ ρ g D 1 ²

Multiplicando por ρ g ambos os lados:

p 1 - p 2 = - ρ V 1 2 2 + 32 L 1 V 1 μ D 1 ²

Substituindo os valores conhecidos:

p 1 - p 2 = - 32 × 0,015 × 3,06 × 0,002 0,25 × 10 - 3 2 - 900 × 3,06 ² 2

p 1 - p 2 = - 51215,2   P a

Isso era esperado pois o escoamento vai de 2 para 1 e não o contrário, logo

p 2 - p 1 = 51215,2   P a

Passo 3

Agora para calcularmos a força F , lembraremos da expressão da pressão:

∆ p = F A

∆ p = p 2 - p 1

A = π D 2 ² 4

Logo

F = ∆ p A

F = p 2 - p 1 π D 2 ² 4

Substituindo os valores:

F = 51215,2 π 1 × 10 - 2 ² 4

F = 4,02   N

Resposta

F = 4,02   N

Exercícios de Livros Relacionados

Óleo SAE 10 a 20°C escoa pelo tubo vertical de 4 cm de diâmetro da figura abaixo. Para a leitura h = 42 cm do manômetro de mercúrio mostrado, (a) calcule a vazão volumétrica em m³/h e (b) determine o
Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145
Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então cor
Para a configuração mostrada abaixo, o fluido é álcool etílico a 20°C, e os reservatórios são muito grandes. Determine a vazão que ocorre em m³/h. O escoamento é laminar?
Vamos resolver o problema P6.25 na forma literal usando a figura abaixo. Todos os parâmetros são constantes, exceto a profundidade Z(t) do reservatório. Determine uma expressão para a vazão Q ( t ) em