Considere o escoamento de fluidos incompressíveis e imiscíveis em regime permanente, entre duas placas paralelas como mostrado na figura ao lado. A placa superior se move a velocidade para a direita enquanto a placa inferior fica parada. Na metade inferior, ou seja, região entre as placas (escoa um fluido com massa específica e viscosidade , e na metade superior escoa outro fluido com massa específica e viscosidade . Admitindo distribuição linear de velocidades nos escoamentos descritos, pedem-se:

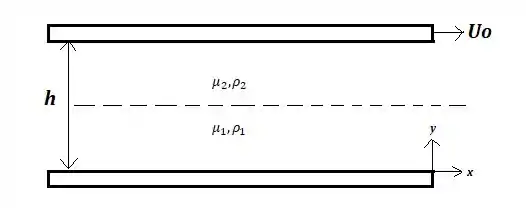
1.1 As condições que as velocidades dos fluidos precisam satisfazer nas paredes e na interface dos fluidos;

Primeiro de tudo vamos lembrar o que são condições de contorno? Bem, quando a gente pega um perfil de velocidade logo após a integração da EDO, a gente costuma ter sempre duas constantes desconhecidas. As condições de contorno são exatamente condições que usamos para obter tais valores das constantes.

Uma condição muito conhecida na mecânica dos fluidos é a condição de aderência, o que isso quer dizer? Bem, que o fluido que está em contato direto com a fronteira do domínio, terá a mesma velocidade dessa fronteira. Então por exemplo, um escoamento dentro de um tubo a gente sabe que nas paredes internas do tubo, a velocidade será zero.

Outra condição muito usada é quando temos dois fluidos imiscíveis em escoamento laminar que possuem uma interface entre eles, onde nessa posição a gente diz que não há escorregamento entre os fluidos, pois as viscosidades são da mesma ordem de grandeza.

Dado essas condições, podemos agora definir as condições pedidas no item 1.1