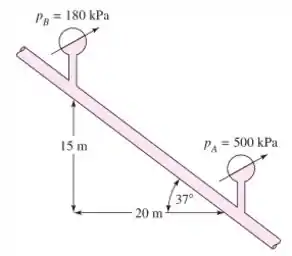
Óleo SAE 30 a escoa no tubo de de diâmetro da Figura que está inclinado a . Para as medidas de pressão mostradas, determine (a) se o escoamento é para cima ou pata baixo e (b) a vazão em .
Passo 1
Fala pessoal, então nesse exercício a gente vai aplicar a equação da energia de novo, mas dessa vez vamos ficar atentos pra cada lado da equação, da entrada e saída.
A princípio não sabemos quem é entrada e quem é saída, então vamos supor que seja a entrada do escoamento. Vem comigo!
Propriedades do óleo SAE 30 a :
Passo 2
Aplicamos a equação da energia:
Valores que conhecemos pelo enunciado e pelo desenho:
Como não há mudança na seção transversal do duto, . O que deixa nossa equação com a cara:
Como não conhcecemos :
Substituindo tudo:
Se a perda de carga é positiva isso quer dizer que nossa suposição inicial estava correta, o escoamento é de até ! Portanto é para cima.
Passo 3
Para determinarmos a vazão devemos conhecer a velocidade do escoamento e a área transversal do duto:
Comecemos pela área, que é circular:
Para a velocidade, lembramos da expressão da perda de carga para o caso laminar:
Como queremos :
Podemos calcular , ou por Pitágoras ou por trigonometria, já que temos o ângulo de , mas se olharmos bem temos um triângulo 3,4,5 ou no caso 15,20,25, logo
Substituindo os valores conhecidos:
Substituindo na expressão da vazão:
Para convertemos para basta multiplicarmos por :
Resposta
Letra a) Escoamento é para cima
Letra b)