UPS – Mecânica dos fluidos – 2018.1 – P1. 1.3
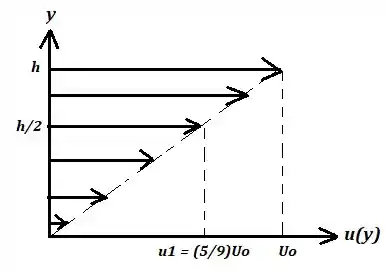
Considere o escoamento de fluidos incompressíveis e imiscíveis em regime permanente, entre duas placas paralelas como mostrado na figura ao lado. A placa superior se move a velocidade para a direita enquanto a placa inferior fica parada. Na metade inferior, ou seja, região entre as placas (escoa um fluido com massa específica e viscosidade , e na metade superior escoa outro fluido com massa específica e viscosidade . Admitindo distribuição linear de velocidades nos escoamentos descritos, pedem-se:
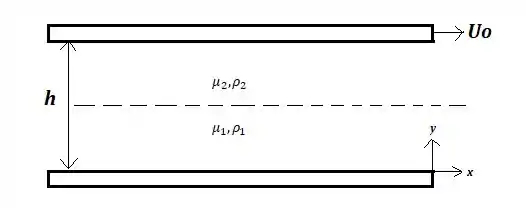
1.3. Admitindo, agora, que , faça um esboço da distribuição das velocidades na forma para
Passo 1
O que que a gente pode fazer? Bem, a gente já sabe que o perfil será linear, certo? Então teremos uma reta onde são conhecidos 3 pontos de velocidade, nas paredes das placas e na interface!
WTFFFF, COMO ASSIM NA INTERFACE? PERA!!! VEM COMIGO!!
Passo 2
Bem, sabemos que o perfil de velocidade na região 1 é dado por:
Na interface a gente tem que
Substituindo, o que a gente vai ter
E como o enunciado nos disse que podemos fazer essa substituição e obter a velocidade na interface apenas em função da viscosidade do fluido 1.
Passo 3
Então bora fazer nosso esboço de gráficoooo!!
A gente sabe que pela condição de aderência que em , temos e que em , . E agora, a partir do que obtemos no passo 2, também sabemos a velocidade na interface!!!
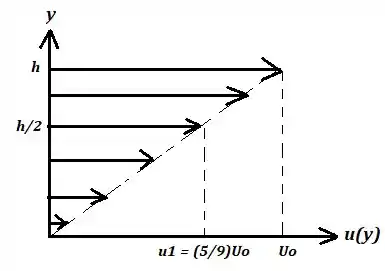
Resposta
