Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Escoamento Laminar e Turbulento e Perda de Carga

Ver Teoria
Exercício 12345678910111213141516171819

Enunciado

A fim de determinar a viscosidade de um líquido de densidade 0,95, você preenche, a uma profundidade de 12 cm, um grande recipiente com drenagem por um tubo vertical de 30 cm de comprimento fixado ao fundo. O diâmetro do tubo é 2 mm, e a taxa de drenagem é 1,9 cm³/s. Qual é o valor da viscosidade do fluido? O escoamento no tubo é laminar?

Passo 1

Neste exercício não temos uma imagem para nos ajudar, portanto vamos esquematizar o problema.

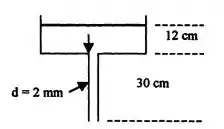
A superfície de entrada é a do topo do tanque e a de saída o tubo final.

Isso nos dá os seguintes valores de entrada e saída que usaremos na nossa equação da energia:

e n t r a d a V 1 = 0 z 1 = 42   c m p 1 = 0

Mas por quê V 1 = 0 ?

Isso é válido para qualquer superfície de controle que apesar de ter uma vazão Q , temo uma área A 1 tão grande que a velocidade que a superfície se move é desprezível.

No caso de p 1 = 0 , estamos trabalhando com pressão manométrica e não a absoluta. Caso fossemos trabalhar com a absoluta utilizaríamos a pressão atmosférica.

Para a sáida temos:

s a í d a V 2 = Q / A 2 z 2 = 0 p 2 = 0

Um líquido ter densidade   0,95 significa:

ρ l í q u i d o ρ á g u a = 0,95

Supondo que ρ á g u a = 1000 k g m 3

ρ l í q u i d o = 950   k g / m ³

Passo 2

Vamos então calcular V 2 = Q / A 2 e substituir os valores do Passo 1, na equação da energia:

V 2 = Q / A 2

V 2 = Q π d ² 4

V 2 = 4 1,9 × 10 - 6 π 2 × 10 - 3 ²

V 2 = 0,605   m / s

Dada a equação da energia:

p 1 ρ g + V 1 ² 2 g + z 1 = p 2 ρ g + V 2 ² 2 g + z 2 + h p

Substituímos o que já conhecêmos:

0 + 0 + 0,42   m = 0 + 0,605 ² 2 × 9,81 + 0 + h p

Logo,

h p = 0,42 - 0,605 ² 2 × 9,81

h p = 0,4   m

Passo 3

Devemos lembrar da expressão da perda de carga

h p = f L d V ² 2 g

Em que,

f = 64 R e d = 64 ρ V d μ

Como não sabemos se o escoamento é laminar ou não vamos calcular o número de Reynolds, que deve ser menor que 2300 no caso laminar:

R e d = ρ V d μ

R e d = 950 × 0,605 × 0,002 μ < 2300

Logo,

μ > 950 × 0,605 × 0,002 2300

μ > 5 × 10 - 4   k g / ( m . s )

Curiosamente quase todos líquidos se encontram acima deste valor de viscosidade. Normalmente, apenas gases tem viscosidades menores que este valor. Portanto para quase todo líquido este escoamento é laminar.

Obs: Isso não é uma informação que você devia ter nascido junto, fica tranquilo. Mas é bom a gente começar a entender as ordens de grandeza de viscosidade. Gases são 10 - 5 , líquidos 10 - 3 , mais ou menos em torno disso.

Portanto podemos utilizar a expressão que conhecemos para o fator de atrito:

f = 64 R e d

Substituindo na expressão da perda de carga:

h p = 64 R e d L d V ² 2 g

h p = 64 μ ρ V d L d V ² 2 g

Rearranjando em função de μ :

μ = h p ρ g d ² 32 V L

Substituindo os valores, sendo L = 30   c m = 0,3   m :

μ = 0,4 × 950 × 9,81 × ( 0,002 ) ² 32 × 0,605 × 0,3

μ = 2,57 × 10 - 3   k g / ( m . s )

Como já tinhamos hipotetizado o escoamento como sendo laminar, confirmamos a hipóstese:

μ > 5 × 10 - 4   k g / ( m . s )

2,57 × 10 - 3 > 5 × 10 - 4   k g / ( m . s )

Escoamento laminar.

Resposta

μ = 2,57 × 10 - 3   k g / ( m . s )

Escoamento é laminar.

Exercícios de Livros Relacionados

Óleo SAE 10 a 20°C escoa pelo tubo vertical de 4 cm de diâmetro da figura abaixo. Para a leitura h = 42 cm do manômetro de mercúrio mostrado, (a) calcule a vazão volumétrica em m³/h e (b) determine o
Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145
Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então cor
Para a configuração mostrada abaixo, o fluido é álcool etílico a 20°C, e os reservatórios são muito grandes. Determine a vazão que ocorre em m³/h. O escoamento é laminar?
Vamos resolver o problema P6.25 na forma literal usando a figura abaixo. Todos os parâmetros são constantes, exceto a profundidade Z(t) do reservatório. Determine uma expressão para a vazão Q ( t ) em