Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Escoamento Laminar e Turbulento e Perda de Carga

Ver Teoria
Exercício 91234567810111213141516171819

Enunciado

UPS – Mecânica dos fluidos – 2019.2 – P1. 1a

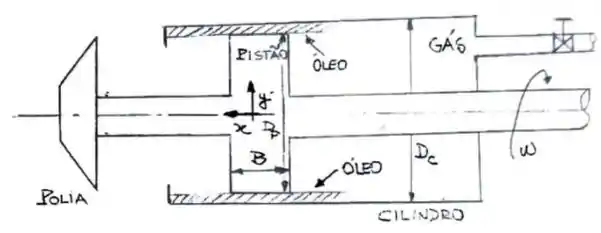
Um dispositivo posicionador de uma polia utiliza um cilindro com diâmetro interno Dc com um pistão em seu interior com diâmetro Dp, conforme esquema da figura. Os movimentos de rotação e de translação do pistão são lubrificados por filme fino de óleo.

São conhecidos:

  • Viscosidade cinemática do óleo, v = 5 × 10 - 5   m 2 / s
  • Massa específica do óleo ρ = 800   k g / m ³
  • Diâmetro do cilindro, D c = 100   m m e do pistão, D p = 99   m m
  • Comprimento do cilindro, B = 100   m m
  • Rotação do cilindro: 6000   r p m
  • Desprezar o atrito entre o eixo girante, onde o pistão está vinculado, e o cilindro

Pede-se:

  1. Para situação de equilíbrio longitudinal (na direção x), em que o único movimento é de rotação, determinar uma expressão literal que permite calcular a potência dissipada no atrito viscoso que ocorre no óleo em função da velocidade angular ω ,   D c ,   D p ,   v   e ρ . Apresente as hipóteses adotadas.

Passo 1

Vamos adotar nossas hipóteses pra começarmos a meter a mão na massa, beleza?

Vamos considerar então:

  1. Lâmina de óleo de espessura muito pequena, ou seja, podemos considerar um perfil linear de velocidade dentro dessa espessura.
  2. Excentricidade do cilindro e do pistão desprezível, pois a espessura de camada de óleo pode ser considerada constante.
  3. Regime permanente, o que implicará que a velocidade angular é constante

A potência será calculada como sendo:

P o t = C   ω

Onde esse “C” é o conjugado que é obtido a partir da força de cisalhamento. Então nossa ideia é encontrar esse cara, pois conhecemos o valor da velocidade angular.

Passo 2

Como a espessura de óleo é pequena, temos o perfil de velocidade linear, o que implica dizer que

τ = μ d v d y = ρ ν Δ v Δ y

Note que v = μ ρ

A diferença de velocidade será dada pela velocidade angular até a outra extremidade onde se tem a condição de não deslizamento, certo?

Δ v = ω D p 2 - 0

Logo, temos que:

τ = ρ v ω D p 2 Δ y

Mas quem é Δ y ? É a diferença do tamanho dos raios, certo?

Δ y = D c - D p 2

Ok, chegamos a conclusão então que:

τ = ρ ν ω D p D c - D p

Passo 3

Na forma diferencial, sabemos que a força cisalhante é dada por:

d F = τ d A

Ao integrar considerando área constante, temos:

F = τ A

Onde a área é dada por: A = 2 π r B = D p π B

Consequentemente a força cisalhante é:

F = π ρ ν ω D p 2 B D c - D p

Passo 4

O conjugado é dado pela seguinte fórmula:

C = F R = F D p 2

Logo,

C = π ρ ν ω D p 3 B 2 D c - D p

Por fim, a potência então pode ser calculada:

P o t = C ω = π ρ ν ω 2 D p 3 B 2 D c - D p

Resposta

P o t = C ω = π ρ ν ω 2 D p 3 B 2 D c - D p

Exercícios de Livros Relacionados

Óleo SAE 10 a 20°C escoa pelo tubo vertical de 4 cm de diâmetro da figura abaixo. Para a leitura h = 42 cm do manômetro de mercúrio mostrado, (a) calcule a vazão volumétrica em m³/h e (b) determine o
Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145
Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então cor
Para a configuração mostrada abaixo, o fluido é álcool etílico a 20°C, e os reservatórios são muito grandes. Determine a vazão que ocorre em m³/h. O escoamento é laminar?
Vamos resolver o problema P6.25 na forma literal usando a figura abaixo. Todos os parâmetros são constantes, exceto a profundidade Z(t) do reservatório. Determine uma expressão para a vazão Q ( t ) em