Considere o escoamento de fluidos incompressíveis e imiscíveis em regime permanente, entre duas placas paralelas como mostrado na figura ao lado. A placa superior se move a velocidade para a direita enquanto a placa inferior fica parada. Na metade inferior, ou seja, região entre as placas (escoa um fluido com massa específica e viscosidade , e na metade superior escoa outro fluido com massa específica e viscosidade . Admitindo distribuição linear de velocidades nos escoamentos descritos, pedem-se:
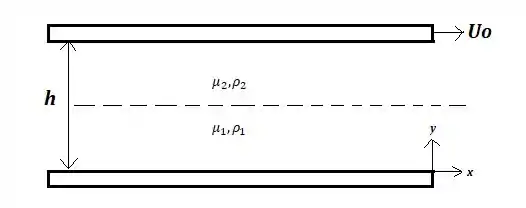
1.2. As distribuições de velocidades das regiões 1 e 2: para e para
Passo 1
Bem, o enunciado nos deu uma dica muito super e mega valiosa que é: assuma distribuição linear de velocidade!!! Opaaaa, isso já nos diz o seguinte, de alguma forma eu vou precisar encontra distribuição de velocidades nas quais devem ter a cara de uma equação linear, ou seja, uma equação da reta do tipo .
Além disso, quando temos uma distribuição linear, a tensão de cisalhamento pode ser descrita na forma de variação , ou seja, ao invés de escrevermos que:
E quem é esse na região 1?
A gente igualou isso a uma constante, pois a velocidade e são constantes, além da própria viscosidade do fluido, certo?
Podemos fazer algo semelhante para a região 2,
Note que na região 2 temos um , uma vez que a placa está a uma velocidade e o fluido dentro do tubo está a velocidade
Passo 2
Na interface, sabemos que uma das condições é não escorregamento, ou seja, e como são valores constantes, seguimos que , não importando qual seja o valor de y que estejamos olhando na região dentro do tubo, beleza?
Temos então que:
Integrando, temos:
Onde podemos utilizar a condição de aderência para calcular C1, tal que em
Fazendo o mesmo para a região 2, temos:
Também utilizando a condição de aderência, temos que em , e portanto, temos que:
Passo 3
Agora vamos olhar para nossa interface entre os fluidos, nessa região a gente sabe que
Ou seja, substituindo as constantes nos perfis de velocidade, temos:
Qual a finalidade estar se fazendo essa contarada toda? Bem, a gente precisa encontrar o valor de C para obtermos o perfil de velocidade por completo. Note que quando , portanto quando igualarmos esses dois perfis, precisaremos substituir
Portanto, ao final temos que os perfis de velocidade são: