Óleo SAE 10 a 20°C , escoa no interior do tubo vertical liso de 30 mm de diâmetro interno mostrado na figura. O desnível do manômetro de mercúrio é de 420 mm, conforme mostrado na figura. A aceleração da gravidade é de 9,8 m/s². Determine:
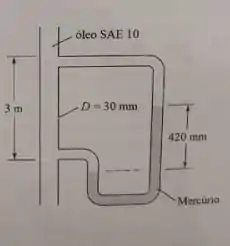
- Partindo das equações integrais de conservação de massa e quantidade de movimento, obtenha o perfil de velocidades do escoamento. Desenvolva a expressão literal e substitua os valores no final.
Passo 1
Para tirarmos o perfil de velocidade, vamos inicialmente considerar o escoamento plenamente desenvolvido, em regime permanente, num tubo vertical de raio . Como temos o movimento na direção , podemos escrever a equação da quantidade de movimento nesta direção, certo?
Onde os dois termos do lado direito são cancelados por conta das nossas hipóteses, beleza? Ao final então a gente tem:
Passo 2
Vamos agora admitir que nosso escoamento é axissimétrico, ou seja, e analisaremos um Vc que é um anel circular diferencial, se liga no desenho ai abaixo, onde a região pontilhada é o volume de controle, VC.
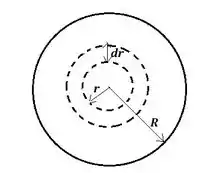
Agora olhando pra esse desenho, quais são as forças que estão atuando sobre nosso volume de controle?
Note que esse desenho é como se você estivesse olhando o volume de controle por cima, mas ele tem também a parte debaixo que é a base desse Vc e as laterais também. Então vamos lá, quais são as forças que atuam na face superior e inferior desse Vc? Você concorda comigo que são as forças normais à superfície? E que força normal é essa? TCHARAAAAMMMM, a força de pressão, que é dada por , certo?
Pois bem, na superfície superior, temos então:
Na superfície da base desse Vc nós teremos a pressão p, mais um gradiente de pressão, certo?
Passo 3
Agora, analisa comigo as paredes desse volume de controle. Não tem mais forças normais atuando nessas paredes, pelo contrário, agora nós temos forças cisalhantes que estarão atuando, pois são forças paralelas à superfície causadas pelo próprio escoamento do fluido.
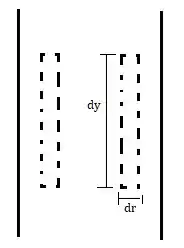
A força de tensão cisalhante é dada por:
Logo, para a parede interna temos:
Note que aqui temos um sinal de menos por conta da direção do crescimento do eixo radial, que é de dentro pra fora. Como essa força está atuando na direção oposta do crescimento do eixo, temos o sinal negativo.
Para a parede externa, temos:
Passo 4
As forças de corpo por sua vez são dadas por:
Então, o somatório das forças superficiais será dado por:
Lembrando que temos:
Mas você deve tá aí se perguntando, ué...cadê o termo . Esse termo vem lá do dFe quando a gente fizer a distributiva. Bem, dr é um termo infinitesimal muito pequeno, quando a gente fizer drdr = dr², esse termo se torna menor ainda e totalmente desprezível. Por isso a gente some com ele no nosso somatório de forças, ok?
Agora, vamos dividir nossa igualdade por
Passo 5
Como a gente viu, não há escoamento na direção radial, portanto p não varia com r e podemos integrar em relação a r:
Para um fluido newtoniano, temos:
Portanto, substituindo temos:
Integrando mais uma vez, temos:
Passo 6
Agora, precisamos usar condições de contorno pra resolver esse rolê todo aí, certo?
A primeira e mais conhecida de todas é a condição de não deslizamento nas paredes estáticas do tubo, ou seja, .
A outra condição que temos é que, considerando escoamento laminar, tem-se que no centro do tubo , ou também conhecida como “velocidade finita no centro do tubo”.
A condição de velocidade finita, nos dará que
Por sua vez, a condição de não deslizamento dará
Desta forma,
Substituindo os valores dados, temos: