Exercícios Resolvidos de Escoamento Laminar e Turbulento e Perda de Carga

Exercício 13 1 2 3 4 5 6 7 8 9 10 11 12 14 15 16 17 18 19

Enunciado

UPS – Mecânica dos fluidos – 2018.1 – P1. 1.4

Considere o escoamento de fluidos incompressíveis e imiscíveis em regime permanente, entre duas placas paralelas como mostrado na figura ao lado. A placa superior se move a velocidade para a direita enquanto a placa inferior fica parada. Na metade inferior, ou seja, região entre as placas (escoa um fluido com massa específica e viscosidade , e na metade superior escoa outro fluido com massa específica e viscosidade . Admitindo distribuição linear de velocidades nos escoamentos descritos, pedem-se:

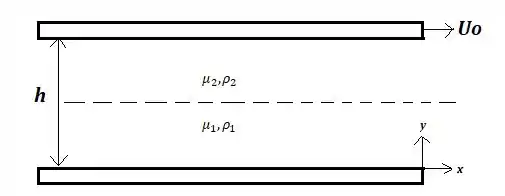
1.4. A tensão de cisalhamento junto à placa inferior em função de , e para a mesma relação entre e do item anterior

Passo 1

Bem, a gente viu no item 1.2. que a tensão de cisalhamento era um valor constante e obtivemos que essa constante era

Considerando a relação de que , temos que:

Mas pera, a gente tinha visto que , ou seja, era constante e não variava com , portanto a tensão de cisalhamento vai ser igual em todo o eixo y, assim tem-se que:

Resposta

Exercícios de Livros Relacionados

Óleo SAE 10 a 20°C escoa pelo tubo vertical de 4 cm de diâmetro da figura abaixo. Para a leitura h = 42 cm do manômetro de mercúrio mostrado, (a) calcule a vazão volumétrica em m³/h e (b) determine o

Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145

Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então cor

Para a configuração mostrada abaixo, o fluido é álcool etílico a 20°C, e os reservatórios são muito grandes. Determine a vazão que ocorre em m³/h. O escoamento é laminar?

Vamos resolver o problema P6.25 na forma literal usando a figura abaixo. Todos os parâmetros são constantes, exceto a profundidade Z(t) do reservatório. Determine uma expressão para a vazão Q ( t ) em