Considere as seguintes afirmações:

(I) se for um espaço vetorial real de dimensão finita munido de um produto interno, for um operador linear e existir uma base ortonormal de tal que a matriz seja diagonal, então o

operador será simétrico;

(II) para qualquer inteiro positivo n e qualquer matriz , se as colunas de formarem uma base ortonormal de com respeito ao produto interno usual, então será igual à matriz identidade, em que denota a transposta da matriz ;

(III) se for um espaço vetorial real de dimensão finita munido de um produto interno e se forem bases ortonormais de , então a matriz será simétrica.

Assinale a alternativa correta:

(a) apenas as afirmações (I) e (II) são verdadeiras;

(b) todas as afirmações são verdadeiras;

(c) apenas as afirmações (II) e (III) são verdadeiras;

(d) apenas a afirmação (III) é verdadeira;

(e) apenas as afirmações (I) e (III) são verdadeiras.

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir qual das afirmações é verdadeira. Bem, vamos começar pela afirmação mais simples. A terceira

A afirmação diz que se for um espaço vetorial real de dimensão finita munido de um produto interno e se forem bases ortonormais de , então a matriz será simétrica.

E aí, vocês acham que é verdade? Parece ser uma afirmação bem forte, né? Pois ela está dizendo que todas as matrizes de mudança de base entre bases ortonormais é simétrica. Vamos tentar dar um contra exemplo. Tome:

e

Ambas as bases são ortogonais, mas temos que

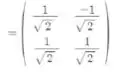
Que não é simétrica. Logo a afirmação (III) é falsa. E como ela é falsa, a única alternativa restante é a letra . Ou seja, as duas primeiras afirmações são verdadeiras.

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊