P4 de Álgebra Linear da UFRJ - 2014.1

Considere o produto interno , , , definido por .

Determine a soma das entradas da projeção ortogonal do vetor na direção do vetor .

Seja uma matriz . Sabendo que então os únicos autovalores possíveis de são:

Quais são todos os valores de para os quais o operador linear dado por NÃO é invertível?

qualquer

é a matriz que realiza a reflexão ortogonal em um subespaço . O autoespaço associado ao autovalor negativo é:

A reta na direção do vetor

A reta na direção do vetor

A transformação linear realiza a reflexão ortogonal dos vetores de pelo plano , seguida da multiplicação por . Então é FALSO afirmar que:

Dimensão do núcleo de é igual a

é diagonalizável

é invertível

e são autovalores de

A dimensão do núcleo de é e seu polinômio característico é . Assinale a alternativa VERDADEIRA:

A dimensão do autoespaço associado ao autovalor é igual a

A matriz é diagonalizável.

A dimensão do autoespaço associado ao autovalor é igual a

Seja uma transformação linear cuja dimensão do núcleo é . A dimensão do espaço ortogonal à imagem de é:

Sejam o espaço vetorial das funções e o operador derivada. Seja , onde é a transformação identidade. Assinale uma função que é autovetor de :

Seja . Indique a alternativa VERDADEIRA

O complemento ortogonal ao espaço gerado pelas colunas de é

O complemento ortogonal ao núcleo de é

O complemento ortogonal ao núcleo de é

O complemento ortogonal ao espaço gerado pelas linhas de é

Seja uma projeção na reta e uma reflexão pela reta . Qual o polinômio característico de ?

Considere o sistema , onde pode ser um vetor qualquer. Sabendo que os autovalores de são e , podemos afirmar que:

O sistema nem sempre tem solução

O sistema tem sempre solução única

O sistema tem sempre mais de uma solução

O sistema nunca tem solução

Seja a reta que melhor ajusta os dados da tabela abaixo, no sentido dos mínimos quadrados.

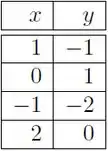
Então o coeficiente vale:

Seja uma transformação linear com determinante nulo. O que podemos afirmar sobre ?

é uma expansão homogênea

é uma rotação

não é uma projeção ortogonal

não é uma reflexão ortogonal

Uma matriz é dita ortogonal se a sua matriz inversa é igual a sua matriz transposta. A matriz é:

simétrica e invertível, mas não é ortogonal

simétrica, invertível e ortogonal

ortogonal e invertível, mas não é simétrica

simétrica, mas não é ortogonal e nem é invertível

Seja e . Considere a forma quadrática dada por e assinale a afirmativa VERDADEIRA

Existe tal que

Existem e tal que e

para todo

para todo