P4 de Álgebra Linear da UFRJ - 2013.1

Considere no espaço vetorial (isto é, os polinômios de grau ) o produto interno dado por . O complemento ortogonal de é:

O espaço gerador por

O espaço gerador por

O espaço gerador por

O espaço gerador por

Suponha que a matriz é e que o seu núcleo é o plano . Assinale a afirmativa VERDADEIRA:

O núcleo de é o plano

O núcleo de é a reta na direção do vetor

A imagem de é a reta na direção do vetor

A imagem de é a reta na direção do vetor

Seja uma transformação linear que multiplica o vetor por e o vetor por . Seja a matriz de na base canônica. Calcule a soma dos elementos da primeira linha de .

Seja a reflexão ortogonal pelo plano . Os autovalores de são:

, e

, e

, e

, e

Considere a matriz . Quais são os seus autovalores?

, e

, e

, e

, e

Sejam um espaço vetorial com produto interno e o conjunto linearmente independente e seja a projeção de em . Então:

é ortogonal a

é ortogonal a

Considere o produto interno usual de . Calcule a projeção ortogonal do vetor na reta que passa pela origem e possui a direção do vetor .

O conjunto solução do sistema abaixo é:

Um conjunto tridimensional em

Um ponto em

Um plano em

Uma reta em

Seja . O vetor é um autovetor associado ao autovalor . O valor de é:

Seja um espaço vetorial e e duas bases distintas de . Sejam e duas transformações lineares distintas. Denotamos a matriz de na base por . Podemos sempre afirmar que:

A equação que modela um determinado fenômeno físico é dada pela função . Alguns experimentos foram realizados com os seguintes resultados:

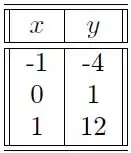
Os valores de , de forma a obter a melhor aproximação no sentido dos mínimos quadrados são:

Sejam e subespaços quaisquer do espaço vetorial . Assinale a alternativa FALSA:

pode ser igual a

sempre é um subespaço de

nunca é um subespaço de

Seja . Qual das matrizes poderia ser a inversa de ?

Calcule a soma das coordenadas do vetor na base

Seja uma transformação linear, , cuja imagem é a reta e o núcleo é o plano de equação . Assinale uma matriz que representa esta transformação linear:

Seja a Reflexão Ortogonal pelo plano . A matriz desta transformação linear na base canônica é:

Se não pertence à imagem de então:

tal que