P4 de Álgebra Linear da UFRJ - 2013.2

Seja a reta que melhor ajusta os dados da tabela abaixo, no sentido dos mínimos quadrados.

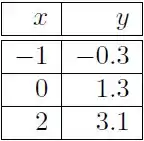
Então o coeficiente vale:

Considere o sistema linear , onde é uma matriz e . Sem conhecer e , mas apenas a forma escalonada da matriz aumentada do sistema,

Nós não podemos afirmar que:

A terceira entrada de qualquer solução de é

admite infinitas soluções

admite solução

Seja o ponto de interseção do plano com a reta . A soma das entradas de é:

Seja . A matriz que, ao multiplicar um vetor qualquer , resulta nas coordenadas de com relação à base é

É dado que . Podemos afirmar que:

Seja linear tal que e . A primeira coluna da matriz de com relação à base canônica é:

Seja o ponto do plano mais próximo de . A distância de a é:

A matriz tem autovalores e . Então é igual a:

Seja o espaço dos polinômios de grau menor ou igual a . Seja a transformação linear dada por . Examine quais das afirmações abaixo são verdadeiras. (Sugestão: monte a matriz da transformação na base canônica de .)

1. é diagonalizável;
2. é invertível.

é falsa e é verdadeira

é verdadeira e é falsa

Ambas são falsas

Ambas são verdadeiras

Considere o espaço munido do produto interno usual. Defina o subespaço vetorial gerado pelo vetor . O seguinte conjunto é uma base para :

Seja

com reais arbitrários. Então:

Seja o sistema linear

com . É falso afirmar que:

Se e , o sistema não admite soluções.

Se e , o sistema admite infinitas soluções.

Se , o sistema admite solução única.

Se e , o sistema não admite soluções.

Sejam um conjunto linearmente independente em e o espaço gerado por este conjunto. Seja ainda . Considere as afirmações:

1. O conjunto é linearmente independente.
2. O conjunto é linearmente independente.

Então:

ambas são verdadeiras

ambas são falsas

é verdadeira e é falsa

é falsa e é verdadeira

Seja . Então:

Existem dois vetores de que, junto com , geram

gera

Quaisquer dois vetores de , junto com , geram

Existem dois vetores de que, junto com geram

Seja uma transformação linear, onde é um espaço vetorial de dimensão finita. Considere as seguintes aformações:

1. Se é linearmente dependente, então é linearmente dependente.
2. Se é linearmente dependente, então é linearmente dependente.

Então:

é verdadeira e é falsa

é falsa e é verdadeira

ambas são falsas

ambas são verdadeiras