UFSC – Lista 3.6 – 2021.1 – P2a
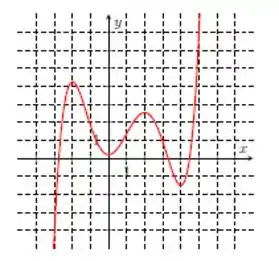
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
Passo 1
E aí, galerinhaaa! Bora relembrar de alguns conceitos importantes que o enunciado pede?
Primeiro, ponto crítico é aquele ponto onde a derivada será igual a zero, ou seja, ele costuma ser no local quando a reta muda de inclinação (de crescente se torna decrescente). Ponto crítico é o ponto onde isso acontece.
E quando não teremos derivada? Quando não temos uma função contínua, ou seja, a função meio que tem uma descontinuidade, e aí naquele ponto, ela não será derivável, show?
Passo 2
Olhando para nosso gráfico, podemos perceber que a função é contínua, portanto, derivável. Os pontos críticos e números críticos são então aqueles onde temos a mudança de inclinação da nossa reta, que eu vou marcar de azul.
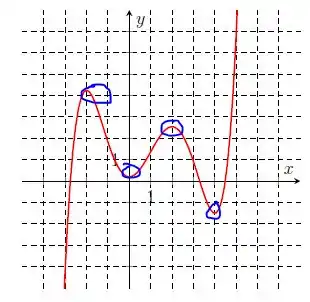
Resposta
Explicação