Lista de Exercicios - UnB de Cálculo 1 da UnB - Lista 12

1) Calcule as integrais definidas abaixo.

a)

1) Calcule as integrais definidas abaixo.

b)

1) Calcule as integrais definidas abaixo.

c)

Calcule as integrais definidas

Calcule as integrais definidas

Calcule as integrais definidas

Calcule as integrais definidas abaixo

Calcule as integrais definidas abaixo

Calcule as integrais definidas abaixo

Calcule as integrais definidas abaixo

Calcule as integrais definidas abaixo

Calcule as integrais definidas abaixo

Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo

Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo

Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo

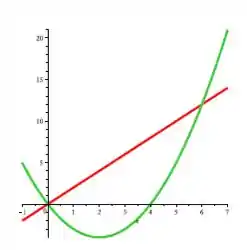
Se e são funções contínuas e em , então a área da região compreendida acima do gráfico de e abaixo do gráfico de é dada por . Nos itens abaixo, vamos calcular esta área para o caso em que e

1. Determine as soluções da equação , chamando de o menor valor e o maior.
2. Pelo Teorema do Valor Intermediário temos que, em todo intervalo , uma das funções é sempre maior ou igual a outra. Determine qual delas é a maior, calculando cada uma delas em um ponto e comparando os dois valores
3. Determine agora a área integrando, no intervalo , a função que está por cima menos a que está por baixo

Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:

Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:

Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:

Repita o argumento acima para as funções abaixo. Neste caso, você encontrará 3 raízes para a equação , digamos . A área agora será calculada como a soma de duas integrais, uma do tipo e outra . Em cada uma delas, você deve integrar a função que está por cima, menos a que está por baixo do intervalo de integração

Repita o argumento acima para as funções abaixo. Neste caso, você encontrará 3 raízes para a equação , digamos . A área agora será calculada como a soma de duas integrais, uma do tipo e outra . Em cada uma delas, você deve integrar a função que está por cima, menos a que está por baixo do intervalo de integração

Se é contínua em , então o Teorema fundamental do Cálculo afirma que a derivada da função é igual a no intervalo . Vamos usar este resultado para calcular a derivada da função

1. Verifique que, se e , então
2. Use a regra da cadeia e o Teorema Fundamental do Cálculo para determinar

Verifique que as funções abaixo não dependem de . Note que, procedendo como acima, é possível fazer isso sem saber a primitiva das funções que estão integradas

Verifique que as funções abaixo não dependem de . Note que, procedendo como acima, é possível fazer isso sem saber a primitiva das funções que estão integradas