UnB – Cálculo 1 – Lista de Exercícios 12 – Questão 2b
Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo
Passo 1
Fala pessoal, tudo bem por aí? Essa questão parece complicada, mas vou te ajudar!
O problema nos pediu para calcular essa integral aqui
Mas utilizando o gráfico! Mas como assim?
Isso mesmo! Integrar uma função em um intervalo fechado, digamos , é equivalente encontrar a área que essa função faz com o eixo horizontal dentro desse intervalo!
Então a ideia aqui é esboçar essa função, que no nosso caso é
Entre o intervalo
E usar as fórmulas de áreas que conhecemos!
Vamos começar?
Passo 2
Nossa função é
Para ter uma ideia do gráfico, vamos substituir e manipular um tantinho
Agora sim! Essa equação já é mais familiar: é a equação de um círculo centrado na origem e de raio !
Então um esboço para a função de até está aqui:
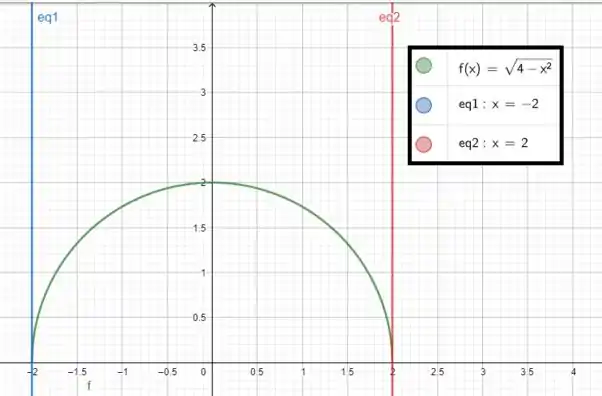
Vemos que entre a função verde e o eixo horizontal, temos um semicírculo! No próximo passo vamos calcular essa área!
Bora lá?
Passo 3
Agora vamos calcular a área! A área de um círculo de raio é
Beleza? Nossa área é um semicírculo (metade da área ) de raio :
Tudo bem até aqui? Agora para achar a integral basta igualar à área:
E é isso! Calculamos a integral sem ter usado técnica! Lembrar que a integral é também uma área pode facilitar (e muito) nossa vida!
Espero ter ajudado! Até a próxima!