UnB – Cálculo 1 – Lista de Exercícios 12 – Questão 5a
Repita o argumento acima para as funções abaixo. Neste caso, você encontrará 3 raízes para a equação , digamos . A área agora será calculada como a soma de duas integrais, uma do tipo e outra . Em cada uma delas, você deve integrar a função que está por cima, menos a que está por baixo do intervalo de integração
Passo 1
Fala pessoal, tudo certinho? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essas duas funções aqui
E pediu para encontrarmos a área entre as curvas!
Para isso o problema anterior nos pediu uma série de itens:
- Encontrar onde as funções de cruzam e assim achar os limites de integração
- Depois escolher um ponto que esteja compreendido entre o intervalo de integração e substituir nas duas funções: assim vamos achar quem está por cima e por baixo
- E por fim vamos integrar!
e é isso que vamos fazer! Mas relaxa que vou resolver passo a passo com você!
Vamos começar?
Passo 2
Vamos começar igualando as duas funções!
Igualando as funções temos:
Daqui temos três soluções
Os valores máximo e mínimo são os nossos extremos (superior e inferior) de integração
Mas como aas funções se cruzam em mais um ponto no meio desse intervalo (em ), precisamos saber quem está por cima e quem está por baixo em cada pedaço!
Beleza?
Passo 3
Agora vamos analisar as duas funções no intervalo e , assim vamos saber quem está por cima e quem está por baixo!
As funções são
Um ponto no intervalo fechado pode ser o (mas vale para qualquer outro nesse intervalo, ok?) temos que
Assim temos , ou seja, a reta está por baixo da função de terceiro grau, tudo bem?
Agora vamos ver em um ponto entre e , como por exemplo :
Assim temos que , a reta está agora por cima da função e terceiro grau! Elas inverteram!
E podemos ver isso bem direitinho no gráfico:
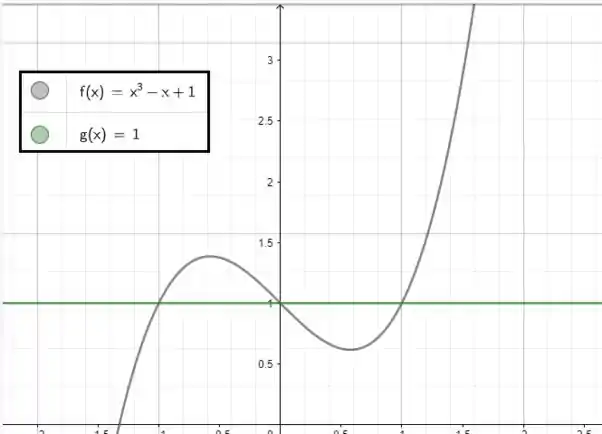
Notem que na hora de integrar vamos precisar dividir essa região em duas partes: de até 0, depois de 0 até 1. E precisamos prestar bem atenção qual função está por cima e qual está por baixo!
Tudo bem até aqui?
Passo 4
Agora que sabemos que a está por cima no primeiro pedaço e embaixo no segundo, #partiu integrar? As funções são
A área vai ser:
Temos duas integrais para resolver! #partiu integrar
E substituir nos limites:
E é isso! Espero ter ajudado!