UnB – Cálculo 1 – Lista de Exercícios 12 – Questão 4b
Proceda como no exercício anterior para calcular a área da região limitada pelas curvas dadas:
Passo 1
Fala pessoal, tudo certinho? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essas duas funções aqui
E pediu para encontrarmos a área entre as curvas!
Para isso o problema anterior nos pediu uma série de itens
- Encontrar onde as funções de cruzam e assim achar os limites de integração
- Depois escolher um ponto que esteja compreendido entre o intervalo de integração e substituir nas duas funções: assim vamos achar quem está por cima e por baixo
- E por fim vamos integrar!
e é isso! Mas relaxa que vou fazer passo a passo com você!
Vamos começar?
Passo 2
Vamos começar igualando as duas funções!
Daí temos
Daqui temos duas soluções
Então as curvas se cruzam nesses dois pontos!
Assim esse é nosso intervalo (e nossos limites de integração)
Beleza?
Passo 3
Agora vamos analisar as duas funções em algum ponto que está dentro do intervalo , assim vamos saber quem está por cima e quem está por baixo!
As funções são
Um ponto no intervalo fechado pode ser o (mas vale para qualquer outro viu?), substituindo nas funções temos
Assim temos , ou seja, a parábola está por cima da reta, como vemos no gráfico:
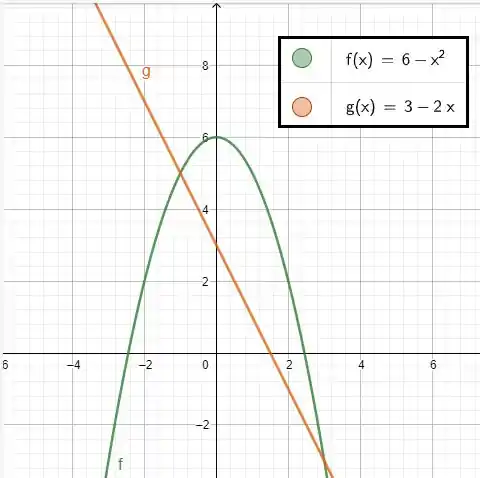
Tudo bem até aqui?
Passo 4
Agora que sabemos que a está por cima, #partiu integrar? As funções são
A área vai ser:
#partiu integrar
E é isso! Espero ter ajudado!