Young & Freedman, Física 2 – Termodinâmica e ondas, 12ª edição, Capítulo 15, Problemas Desafiadores, Questão 82
(Cap. 15. Problemas Desafiadores - Ex.82)Um escafandrista está suspenso abaixo da superfície do Lago Ness por um cabo preso a um barco na superfície do lago (Figura 15.40). O mergulhador e seus equipamentos possuem massa total de e ocupam um volume igual a . O cabo possui diâmetro igual a e a densidade linear . O mergulhador imagina que viu algo se movendo nas profundezas escuras do lago e sacode a extremidade do cabo , produzindo ondas transversais que sobem através do cabo para sinalizar a seus companheiros que estão no barco.
a) Qual é a tensão no cabo em sua extremidade inferior presa ao mergulhador? Não se esqueça de incluir a força de empuxo que a água (densidade igual a ) exerce sobre ele.
b) Calcule a tensão no cabo a uma distância acima do mergulhador. A força de empuxo que a água exerce sobre o cabo deve ser incluída.
c) A velocidade de propagação de uma transversal é dada por equação (15.13). Portanto, a velocidade varia ao longo do cabo, visto que a tensão não é constante. (Esta relação despreza a força de amortecimento que a água exerce sobre o cabo que se move.) Integre para achar o tempo que o primeiro sinal leva para atingir a superfície.
Passo 1
Fala aí gente, tudo belezinha? Espero que sim
Bom, a situação que temos no nosso problema é a de um mergulhador (escafandrista) que está submerso pelas águas do Lago Ness conectado por um cabo que se encontra preso em uma embarcação. De maneira geral, o que precisamos fazer aqui é calcular a força resultante para vários segmentos do cabo de acordo com o que for solicitado nas alternativas. As forças que existem nesse problema são: o peso do mergulhador, o peso do segmento do cabo, a tensão no cabo e a força de flutuação (empuxo).
A força de empuxo de um objeto completamente submerso na água é:
Lembrando que é a densidade da água, é o volume do fluído deslocado e por fim, representa a gravidade.
Passo 2
a)Bom, essa alternativa deseja encontrar a tensão no cabo em sua extremidade inferior presa ao mergulhador. Logo como queremos saber só a tensão na extremidade do cabo, basta olharmos para as forças presentes apenas nessa situação que é a força de tensão no cabo, a força peso do mergulhador e a força de empuxo.
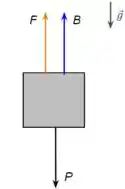
A tensão na extremidade na qual o mergulhador está, pode ser calculada a partir da diferença entre o peso do mergulhador e o empuxo da água.
Substituindo os valores:
Passo 3
b)Agora a questão já deseja saber a tensão no cabo a uma distância acima do mergulhador, ou seja, o que muda aqui em relação ao item (a) é que agora precisamos incluir o peso do cabo que está entre o mergulhador e o ponto .
E a força do cabo é o peso do pedaço do cabo correspondente ao comprimento menos a força de empuxo da água.
Substituindo os valores temos:
Passo 4
c) Primeiramente podemos escrever a função da tensão em relação a da seguinte forma:
De acordo com o enunciado , desta forma a velocidade da onda em função de será:
Fazendo uma separação de variáveis para poder integrar e encontrar o tempo, obtemos:
Substituindo os valores:
E aí bora treinar mais? Logo, você vai tá expert!
Resposta
a)
b)
c)