Livro Young and Freedman, Volume 2, 12ª Edição, Capítulo 15, Seção Exercícios, Exercício 28
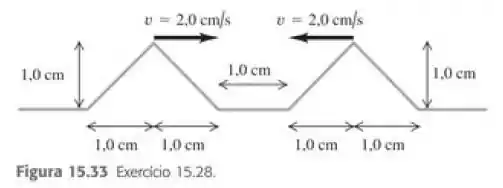
(Capítulo 15.Exercícios – Exercícios 28) Dois pulsos ondulatórios triangulares estão se aproximando em uma corda esticada, como indicado na Figura 15.33. Os dois pulsos são idênticos e se deslocam com velocidade igual a 2,0 cm/s. A distancia entre as extremidades dianteira dos pulsos é igual a 1,0 cm para . Desenhe a forma da corda para
Passo 1
Faaala, pessoal! Tudo certinho? Bora lá resolver mais uma questãozinha!
Bom, o enunciado diz pra gente que temos dois pulsos ondulatórios se aproximando em uma corda esticada, e que eles são idênticos. Tá, mas o que isso quer dizer?
Quando dois pulsos idênticos se aproximam, quando eles se encontrarem havrá uma superposição!! Então, pra resolver essa questão aqui, basta aplicarmos a teoria do princípio de superposição de ondas.
Essa teoria ainda diz pra gente que o deslocamento líquido é a soma algébrica dos deslocamentos devido a cada pulso!
Borá lá trabalhar com essas informações então!
Passo 2
Para sabermos a forma da corda em um determinado tempo, basta fazermos uma interpretação do que está acontecendo!
Nós sabemos que no tempo zero (), a distância entre os dois pulsos é igual a 1,0 cm. Além disso, temos que a velocidade é de .
Então, para cada intervalo de tempo apresentado no enunciado vamos ter:
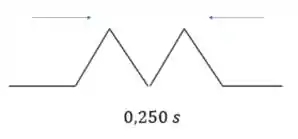
No tempo de 0,5 segundos, as ondas estarão muit próximas uma da outra e teremos uma quase superposição:
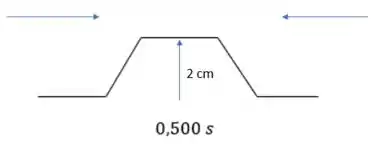
Em 0,75 segundos, já teremos a superposição, tendo uma onda com o dobro da altura, e de mesma forma triangular:
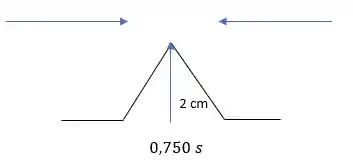
Em 1 segundo, as ondas já se atravessaram e seguem seus caminhos:
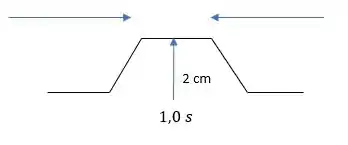
Por fim, em 1,25 segundos, as ondas se atravessam completamente, e voltam a ter 1 cm de altura cada:
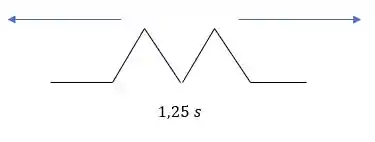
Observe aqui que os pulsos interferem, somando as alturas quando se sobrepõem, mas retomam sua forma original depois que eles passaram completamente um pelo outro.
Prontinho pessoal! Pra essa questão é isso! Bora resolver mais uma?
Resposta
