Exercícios Resolvidos de Interferência de Ondas Sonoras

Exercício 8 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Enunciado

Livro Young and Freedman, Volume 2, 12ª Edição, Capítulo 15, Seção Exercícios, Exercício 29

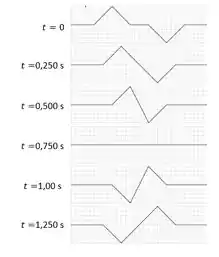
(Capítulo 15.Exercícios – Exercícios 29) Suponha que o pulso que se desloca para a esquerda no Exercicio 15.28 esteja abaixo do nivel da corda não esticada, em vez de acima. Desenhe os mesmo diagramas que voce desenhou naquele exercicio.

Passo 1

Faaala, galera! Beleza? Bora lá resolver mais um exercício!

Bom, aqui vamos aplicar novamente o principio de superposição. Vale ressaltar que o fato da onda da direita estar por baixo não muda que essas ondas continuam em superposição!

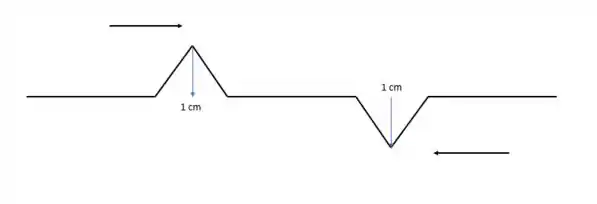
Pra gente entender melhor esse novo esquema, vamos desenhar ele aqui embaixo:

Passo 2

Como a onda que se desloca para a esquerda está para baixo, teremos uma configuração diferente da do exercício anterior.

A forma da corda em cada momento especificado é mostrada nas figuras a seguir:

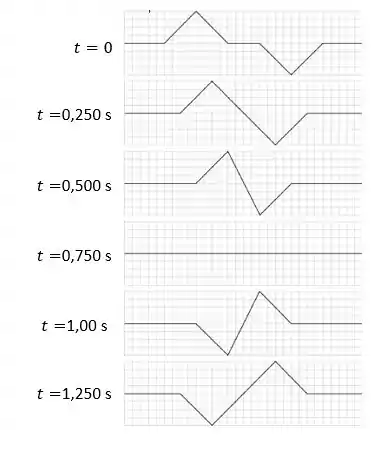
Aqui nós vemos novamente que os pulsos interferem quando se sobrepõem, mas retomam sua forma original depois que eles passaram completamente um pelo outro.

Prontinho, pessoal! Pra essa questão é isso. Bora resolver mais uma?

Resposta

Exercícios de Livros Relacionados

A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s

Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega

Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su

Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase

Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr