Young & Freedman, Física 2 – Termodinâmica e ondas, 12ª edição, Capítulo 16, Exercícios, Questão 33
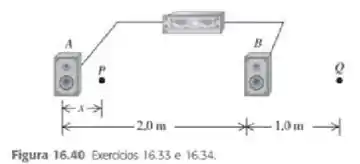
(Cap.16.6 – Ex. 33) Dois alto-falantes, A e B (Figura 16.40), são alimentados por um mesmo amplificador e emitem ondas senoidais em fase. O alto-falante B está a uma distância de à direita do alto-falante A. a velocidade do som no ar é igual a . Considere o ponto Q ao longo da extensão da linha reta que une os dois alto-falantes, situado a uma distância de à direita do alto-falante B. Os dois alto-falantes emitem ondas sonoras que se propagam diretamente dos alto-falantes até o ponto Q. a) Qual é a menor frequência capaz de produzir interferência construtiva no ponto Q? b) Qual é a menor frequência capaz de produzir interferência destrutiva no ponto Q?
Passo 1
Fala aí, beleza?
Bom, então basicamente nossa questão se trata de dois alto-falantes que emitem ondas sonoras que alcançam o ponto Q.
Lembrando que os alto-falantes estão a distâncias distintas do ponto Q.
Com isso, desejamos saber a frequência quando se tem uma interferência construtiva e uma interferência destrutiva.
Bora botar a mão na massa?
Primeiro, precisamos encontrar a diferença de caminho entre as duas fontes sonoras, como as duas fontes e o ponto Q estão todos na mesma linha, então a diferença de caminho entre a onda que sai de A e vai até Q é a onda que sai de B e vai até Q é:
Com esse valor, poderemos encontrar as frequências em que as ondas se somam ou se cancelam no ponto Q.
Passo 2
a) Para calcularmos o caso em que as amplitudes das ondas se somam, ou seja, que produzem interferência construtiva entre si, precisamos usar:
Onde representa a diferença entre as fontes sonoras em relação a um determinado ouvinte que é indicado na nossa questão pelo ponto Q.
Assim,
Sendo n um número inteiro.
Sabemos também, pela equação da velocidade de uma onda que:
Substituindo na primeira equação:
E como queremos a menor frequência possível, deve ser 1, assim:
Passo 3
b) Interferência destrutiva ocorre quando as amplitudes das ondas se subtraem, para o caso de interferência destrutiva entre as duas ondas vindas de cada fonte, usaremos a equação:
Sendo a distância entre as duas fontes sonoras , temos que :
Substituindo de novo:
Isolando a frequência que precisamos achar:
Como estamos procurando a menor frequência, n deve ser 1 de novo:
Substituindo a velocidade do som:
Tudo ok? Bora fazer mais!!!