Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 15 – Exercício 11.
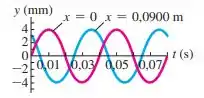
(Cap 15 - Ex 11) Uma onda senoidal propaga-se ao longo de uma corda esticada sobre o eixo . O deslocamento da corda em função do tempo é indicado na figura 15.30 para partículas nos pontos e .
- Qual é a amplitude da onda?
- Qual é o período da onda?
- Informamos a você que a distância entre os pontos e é menor do que o comprimento de onda. Determine a velocidade e o comprimento de onda quando ela se propaga no sentido .
- Supondo agora que a onda se propague no sentido , determine a velocidade e o comprimento de onda.
- Seria possível determinar de forma não ambígua o comprimento de onda calculado dos itens e se você não usasse o dado de a distância entre os pontos ser menor do que o comprimento de onda? Justifique sua resposta.
Passo 1
Olá, tudo bem? Vou ajudar você nessa aqui!
Letra a)
Determinar a amplitude de uma onda é tranquilo pelo gráfico!
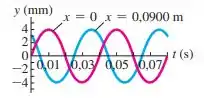
É o maior valor que a onda assume. Dando uma olhada no desenho, vemos que o maior valor que essa onda assume é .
Passo 2
Letra b)
O período é tranquilo de se achar também! É o tempo de um ciclo completo (uma crista mais uma onda). Pelo gráfico vemos que o período é:
Certo até aqui? Blz!
Passo 3
Letra c)
Uma vez que quando temos e , e sabendo que a onda está se propagando na direção de , essa onda pode ser descrita pela seguinte expressão:
Do gráfico, se a onda está se movendo na direção , e se e estiverem dentro de um comprimento de onda, o pico em para se move de modo que no instante (do gráfico, aproximadamente) a onda se move para .
O pico em é o pico anterior em , e corresponde ao primeiro máximo da função de onda, então o argumento do seno vai ser igual a :
E se o mesmo pico se move para em , podemos usar essa informação para determinar a razão :
Mas sabemos que , então o comprimento de onda vai ser igual a:
E assim podemos achar a velocidade da onda:
Passo 4
Letra d)
Se a onda estiver se propagando na direção , então a função de onda é dada por:
Então o primeiro pico é com no instante e o segundo pico é em na origem e corresponde ao argumento . E seguindo os mesmos passos do item anterior, podemos determinar o comprimento de onda e a velocidade. Vamos lá?
Iniciando pelo comprimento da onda, temos:
E a velocidade vai ser:
Passo 5
Letra e)
Não, não saberíamos qual ponto da onda em foi movido para qual ponto em .