Duas ondas senoidais, viajando em direções opostas, interferem para produzir uma onda estacionária descrita por , onde está em e está em . Qual é a distância (em ) entre os dois primeiros anti-nodos?
A)
B)
C)
D)
E)
Passo 1
A primeira coisa que você precisa saber aqui é que a forma da onda estacionária não se move. Ou seja, independente do tempo, ela vai ser sempre a mesma carinha.
Ele tá perguntando a distância entre os primeiros anti-nodos. Anti-nodos são basicamente as “cristas”, que coincidem com os vales. Enquanto os nodos são os pontos médios.
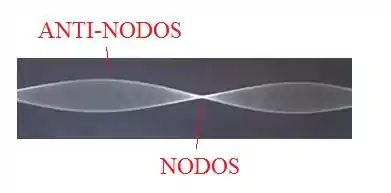
Bom, pela equação da onda dada no enunciado, nós podemos encontrar algumas coisinhas, como é o termo que aparece multiplicado pelo :
Passo 2
Como a distância entre 2 anti-nodos consecutivos é , temos que:
Resposta
Alternativa (d).