A figura abaixo mostra dois alto-falantes separados por uma distância . Um microfone é posicionado a uma distância em frente a um dos alto-falantes. Um sistema de áudio alimenta os alto-falantes em fase com uma frequência fixa . A velocidade do som no local vale . A frequência é, então, varrida no intervalo audível de a .
- Se , em quantos valores de a intensidade sonora é mínima na posição do microfone?
- Determine o maior valor de , em metros, para o qual ocorre um máximo de intensidade na frequência .
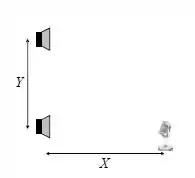
Passo 1
Temos como base o seguinte esquema:
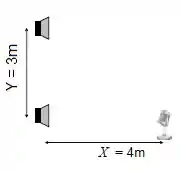
Temos que a diferença de percurso é:
A diferença de fase entre as ondas dos dois alto-falantes pode ser escrita como:
Substituindo por , temos:
Temos mínimos de intensidades nas frequências
onde
A menor delas , está no intervalo audível. Agora 20000/170=117. De modo que Então:
Portanto o número de mínimos é 59.
Passo 2
Para que ocorra um máximo de intensidade na frequência , temos que saber qual é o máximo valor possível de Logo:
Note que quanto maior menor é . Portanto, a menor variação de fase , é em unidades de (condição de máximo). Então:
Passo 3
Resposta
a) 59
b) 4m