Um pulso numa corda é descrito pela função e um segundo pulso, na mesma corda, é descrito por onde são dados em e em segundos.
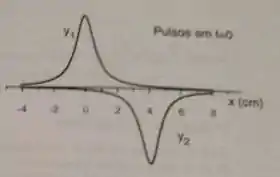
Em que direção cada pulso se propaga? Calcule a velocidade de cada pulso.
Determine em que instante os dois pulsos se cancelam totalmente.
Determine em que ponto os pulsos sempre se cancelam.
Passo 1
Para determinar a velocidade e a direção em que o pulso se propaga, podemos manipular a função dos pulsos para achar e então derivamos em relação ao tempo!
Simbora!
Para o pulso , temos:
Para o pulso , temos:
Portanto, temos que o pulso se desloca para a direita, com velocidade e o pulso se desloca para a esquerda com velocidade .
Passo 2
Para que os pulsos se cancelem, temos que , agora é só isolar o tempo para determinar o instante em que isso ocorre!
Passo 3
Para determinar os pontos em que os pulsos sempre se cancelam, precisamos novamente que , mas nesse caso, precisamos determinar . Vamos fazer o mesmo mimimi que fizemos no item anterior!
Show!
Resposta
,