3. Dada a função :
a) Aplique o método de Newton para encontrar um valor aproximado da raiz de . Para cada iteração, apresente os valores de e . Considere, utilize 4 casas decimais e arredondamento padrão. Utilize como critério de parada 3 iterações () ou .
b) Complemente a implementação do código abaixo para encontrar o zero da função pelo método da Falsa Corda utilizando 50 iterações como critério de parada. Considere o intervalo de separação . OBS: Em C, a equação pode ser escrita como.

Passo 1
Opaa pessoal, tudo bem? Vamos então lembrar do método de Newton! Basicamente é mais um método que parte de um valor inicial e, por meio de várias iterações, chega em uma solução ao atingir o critério de parada! Neste caso, a cada interação devemos calcular o , o e o valor seguinte, isto é, .
Bora começar pela derivada? Bem simples, olha lá:
Passo 2
Em seguida, vamos para as iterações:
Iteração 0:
Iteração 1:
Iteração 2:
Mas olha só: . Como atingimos um critério de parada, podemos interromper as iterações e afirmar que é uma aproximação de raiz de ! Fácil, né?
Passo 3
O método da Falsa Corda é outro método iterativo para encontrar a raiz de uma função! Mas dessa vez queremos fazer 50 iterações, galera. Fica puxado fazer a mão, então um código é o melhor caminho!
Nesse caso, temos um intervalo [a,b] que contém a raiz da função e vamos aproximá-la fazendo:
Depois de obter o , calculamos e verificamos se ou se . Mas pra que isso? Bom galera, existe um cara chamado Bolzano que enunciou o seguinte teorema: um intervalo contém a raiz de uma função se .
Logo, a cada iteração descobrimos um valor mais próximo da nossa raiz e reduzimos o intervalo de entrada! Vamos ficar com um código assim:
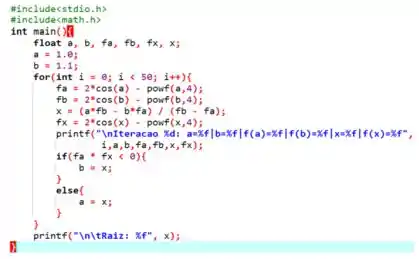
Primeiro fazemos usamos a estrutura de repetição for para percorrer as 50 iterações, uma por uma. Em seguida, calculamos os valores de , , a aproximação da raiz e . Também imprimimos algumas informações importantes: o número da iteração, o intervalo [a,b] atual, e os valores que acabamos de calcular nas linhas anteriores!
No final, damos aquela conferida que eu comentei agora pouco para reduzir o intervalo de entrada! Usando um condicional if/else, definimos se o próximo intervalo de entrada será [a,b=x] ou [a=x,b].
Ao fim das 50 iterações, imprimos o último valor aproximado de ! Moleza!
Resposta
a) Utilizando o critério de parada , obtemos que é um valor aproximado da raiz de .