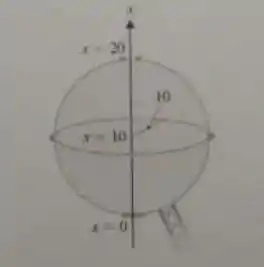
3) Suponha um tanque de água esférico com raio 10 dm conforme a figure abaixo. Determine o nível de água (com erro menor que 1mm) tal que o tanque fique preenchido com 1/3 do seu volume, utilizando para tal o método de Newton. Justifique a convergência do método de Newton.
Passo 1
Falaaa... beleza??
Nessa questão queremos saber qual é o nível da água quando o volume preenchido é 1/3 do volume do tanque.
Pra isso vamos precisar do Volume da esfera:
Do Volume em função da altura:
E vamos usar o método de Newton:
Passo 2
Como temos o raio e queremos achar a altura quando o volume é 1/3 do volume total, então:
Pra resolver essa equação super feiosa temos que usar o método de Newton, então vamos passar tudo pra um lado só e chamar de
E derivando:
Passo 3
Como queremos do volume, então é razoável a gente usar um chute inicial que esteja entre da altura e da metade da esfera. Vamos chutar
Aplicando o método de Newton:
Pra segunda iteração:
Como queremos o erro menor que
Temos
Então o valor de será:
Passo 4
Para a convergência do método de newton devemos verificar duas coisas...
A função que a gente achou deve ser contínua no intervalo que pegamos (que foi entre 1/3 e 1/2 do diâmetro da esfera). A derivada primeira e a derivada segunda também devem ser contínuas nesse intervalo.
A outra coisa �� no intervalo seja diferente de zero. Como:
Que só vai ser zero quando e . Logo é diferente de zero em todo o intervalo que pegamos.
Com isso garantimos que a convergência do Método de Newton.