Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método de Newton-Raphson

Ver Teoria
Exercício 4123567891011121314151617

Enunciado

Encontre as duas raízes reais do polinômio abaixo pelo método de Newton-Raphson com precisão 10 - 5 .

p x = x 4 - 2 x 3 + 4 x - 1.6

Passo 1

Vamos começar encontrando intervalos que contenham elas:

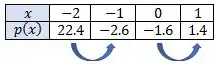
Beleza, achamos nossas duas raízes! Uma no intervalo - 2 , - 1 e outra no intervalo 0,1 .

Passo 2

Intervalo - 2 , - 1

Cálculos Iniciais

f x = x 4 - 2 x 3 + 4 x - 1.6

f ' x = 4 x 3 - 6 x 2 + 4

g x = x - x 4 - 2 x 3 + 4 x - 1.6 4 x 3 - 6 x 2 + 4

x 0 = - 1

ε = 10 - 5

Iteração 1 :

x 1 = g x 0 = - 1.433333

Critério de Parada:

x 1 - x 0 = 0.433333 > 10 - 5

f x 1 = 2.776816 > 10 - 5

Como não alcançamos o critério de parada continuamos as iterações.

x 1 = - 1.433333

ε = 10 - 5

Iteração 2 :

x 2 = g x 1 = - 1.295221

Critério de Parada:

x 2 - x 1 = 0.138112 > 10 - 5

f x 2 = 0.379167 > 10 - 5

Como não alcançamos o critério de parada continuamos as iterações.

x 2 = - 1.295221

ε = 10 - 5

Iteração 3 :

x 3 = g x 2 = - 1.269527

Critério de Parada:

x 3 - x 2 = 0.025694 > 10 - 5

f x 3 = 0.011654 > 10 - 5

Como não alcançamos o critério de parada continuamos as iterações.

x 3 = - 1.269527

ε = 10 - 5

Iteração 4 :

x 4 = g x 3 = - 1.268686

Critério de Parada:

x 4 - x 3 = 0.000841 > 10 - 5

f x 4 = 1 . 2 ∙ 10 - 5 > 10 - 5

Como não alcançamos o critério de parada continuamos as iterações.

x 4 = - 1.268686

ε = 10 - 5

Iteração 5 :

x 5 = g x 4 = - 1.268685

Critério de Parada:

x 5 - x 4 = 8.8 ∙ 10 - 7 < 10 - 5

f x 5 = 1 . 4 ∙ 10 - 11 < 10 - 5

Alcançamos nosso critério de parada. Então x - = - 1.268685 . Repara que nessa alcançamos uma precisão de quase 10 - 11 no nosso resultado final! Isso com apenas 5 iterações.

Passo 3

Intervalo 0,1

Cálculos Iniciais

f x = x 4 - 2 x 3 + 4 x - 1.6

f ' x = 4 x 3 - 6 x 2 + 4

g x = x - x 4 - 2 x 3 + 4 x - 1.6 4 x 3 - 6 x 2 + 4

x 0 = 0

ε = 10 - 5

Iteração 1 :

x 1 = g x 0 = 0.4

Critério de Parada:

x 1 - x 0 = 0.4 > 10 - 5

f x 1 = 0.1024 > 10 - 5

Como não alcançamos o critério de parada continuamos as iterações.

x 1 = 0.4

ε = 10 - 5

Iteração 2 :

x 2 = g x 1 = 0.431068

Critério de Parada:

x 2 - x 1 = 0.031068 > 10 - 5

f x 2 = 0.001401 > 10 - 5

Como não alcançamos o critério de parada continuamos as iterações.

x 2 = 0.431068

ε = 10 - 5

Iteração 3 :

x 3 = g x 2 = 0.431505

Critério de Parada:

x 3 - x 2 = 0.000437 > 10 - 5

f x 3 = 2.8 ∙ 10 - 7 < 10 - 5

Alcançamos nosso critério de parada. Então x - = 0.431505 .

Resposta

Intervalo - 2 , - 1 :   x - = - 1.268685

Intervalo 0,1 : x - = 0.431505

Exercícios de Livros Relacionados

Use o método de Newton para estimar as soluções da equação x 2 + x - 1 = 0 . Comece comx 0=-1 para a solução à esquerda e com x 0=1 para a solução à direita. Depois, determine x 2 em cada caso.
Os gráficos de y= x e y=3-x 2 se cruzam em um ponto x=r . Use o método de Newton para calcular o valor de r com quatro casas decimais.
Nos exercícios de 5 até 10, use o método de Newton para encontrar o valor aproximado da raiz indicada com erro menor que um milésimo. 2 x 4 - 2 x 3 + x 2 + 3 x - 4 = 0 ; a raiz negativa
Nos exercícios de 5 até 10, use o método de Newton para encontrar o valor aproximado da raiz indicada com erro menor que um milésimo. x 4 + x 3 - 3 x 2 - x - 4 = 0 ; a raiz positiva
Explique por que as quatro questões seguintes pedem a mesma informação: Determine as raízes de f ( x )=x 3-3 x-1 . Determine as abscissas da interseção da curva y=x 3 com a reta y=3 x+1 . Determine as