Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método de Newton-Raphson

Ver Teoria
Exercício 2134567891011121314151617

Enunciado

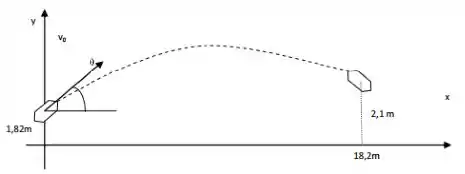
Um jogador de futebol americano está prestes a fazer um lançamento para outro jogador de seu time. O lançador tem uma altura de 1.82 m e o outro jogador está 18.2 m afastado. A expressão que descreve o movimento da bola é a familiar equação da física que descreve o movimento do projétil:

y = x t a n θ - 1 2 x 2 g v 0 2 cos 2 ⁡ θ + h

Onde x e y são as distâncias horizontal e vertical, respectivamente, g = 9.81 m / s 2 é a aceleração da gravidade. v 0 é a velocidade inicial da bola quando deixa a mão do lançador e θ é o ângulo que a bola faz com o eixo horizontal nesse mesmo instante. Para v 0 = 15.2 m / s , x = 18.2 m , h = 1.82 m e y = 2.1 m , determine o ângulo θ no qual o jogador deve lançar a bola.

Resolva o problema com tolerância 10 - 8 rad.

Passo 1

Vamos começar substituindo os valores na fórmula:

2.1 = 18.2 tan ⁡ θ - 1 2 18.2 2 ∙ 9.81 15.2 2 cos 2 ⁡ θ + 1.82

18.2 tan ⁡ θ - 7.03226 cos 2 ⁡ θ - 0.28 = 0

Passo 2

Agora precisamos encontrar um intervalo com a raiz:

f 0 = - 7.31226

f 1 = 3.97568

Então temos uma raiz em 0,1 .

Passo 3

Cálculos Iniciais

f x = 18.2 tan ⁡ θ - 7.03226 cos 2 ⁡ θ - 0.28

f ' x = sec 2 ⁡ θ 18.2 - 14.0645 tan ⁡ θ

g x = x - f x f ' x

x 0 = 0

ε = 10 - 8

Iteração 1 :

x 1 = g x 0 = 0.401772527

Critério de Parada:

x 1 - x 0 = 0.401772527 > 10 - 8

f x 1 = 0.848877897 > 10 - 8

Como não alcançamos o critério de parada continuamos as iterações.

x 1 = 0.401772527

ε = 10 - 8

Iteração 2 :

x 2 = g x 1 = 0.460595698

Critério de Parada:

x 2 - x 1 = 0.05882317 > 10 - 8

f x 2 = 0.012965943 > 10 - 8

Como não alcançamos o critério de parada continuamos as iterações.

x 2 = 0.460595698

ε = 10 - 8

Iteração 3 :

x 3 = g x 2 = 0.461522891

Critério de Parada:

x 3 - x 2 = 0.000927194 > 10 - 8

f x 3 = 3.437 ∙ 10 - 6 > 10 - 8

Como não alcançamos o critério de parada continuamos as iterações.

x 3 = 0.461522891

ε = 10 - 8

Iteração 4 :

x 4 = g x 3 = 0.461523137

Critério de Parada:

x 4 - x 3 = 4.6 ∙ 10 - 8 > 10 - 8

f x 4 = 2.2 ∙ 10 - 10 < 10 - 8

Pronto, achamos o ângulo de lançamento. x - = 0.461523137 .

Resposta

x - = 0.461523137

Exercícios de Livros Relacionados

Use o método de Newton para estimar as soluções da equação x 2 + x - 1 = 0 . Comece comx 0=-1 para a solução à esquerda e com x 0=1 para a solução à direita. Depois, determine x 2 em cada caso.
Os gráficos de y= x e y=3-x 2 se cruzam em um ponto x=r . Use o método de Newton para calcular o valor de r com quatro casas decimais.
Nos exercícios de 5 até 10, use o método de Newton para encontrar o valor aproximado da raiz indicada com erro menor que um milésimo. 2 x 4 - 2 x 3 + x 2 + 3 x - 4 = 0 ; a raiz negativa
Nos exercícios de 5 até 10, use o método de Newton para encontrar o valor aproximado da raiz indicada com erro menor que um milésimo. x 4 + x 3 - 3 x 2 - x - 4 = 0 ; a raiz positiva
Explique por que as quatro questões seguintes pedem a mesma informação: Determine as raízes de f ( x )=x 3-3 x-1 . Determine as abscissas da interseção da curva y=x 3 com a reta y=3 x+1 . Determine as