Se , e (ângulo entre os vetores e ) , calcule o módulo de
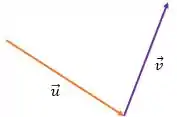
Passo 1
Nesse caso, temos a regra do fechamento o triângulo, uma vez ligando a extremidade de a origem de formamos um triângulo.
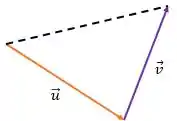
Com isso, para calcular o valor da resultante usamos a formulazinha:
Onde, nesse caso temos:
, e
Passo 2
Substituindo os valores:
Resolvendo:
Belezinha ;)