UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cáclulo 2 - Profº Félix Gómez - Primeira Lista, Questão 1.13
Considere a norma da soma em , então a norma de é dada por
Faça um esboço de uma bola de centro e raio .
Passo 1
Olá pessoaaal, como vocês estão?
Nessa questão recebemos a seguinte definição de norma no :
Se , então:
Ou seja, se tomarmos por exemplo, o vetor:
Então:
Usando essa definição, o problema nos pede para fazer um esboço de uma bola de centro e raio .
O ponto mais importante para sacarmos a ideia dessa questão é entender que apenas pertencerão à bola os pontos cuja norma do máximo com relação ao centro for menor ou igual a , beleza?
Então, vamos usar essa ideia pra matar a questão 😊
Passo 2
Vamos começar imaginando que o ponto esteja na borda da bola de centro . Então, deve valer que:
Se:
Então:
Analisando essa fórmula, temos que o maior e menor valores de ocorrem quando:
Daí, temos:
Abrindo o módulo, vem duas possibilidades para :
E:
Analogamente, maximizando o valor de encontramos:
E:
Daí, temos então pontos na extremidade da nossa bola:
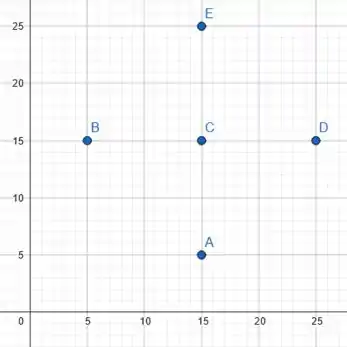
Massa!
Passo 3
Se pensarmos agora em um ponto na borda da circunferência tal que o vetor distância em relação a seja o vetor , devemos ter que:
Então:
Logo:
Podemos abrir essa equação de formas:
Essas retas devem estar justamente ligando os pontos extremos que plotamos antes.
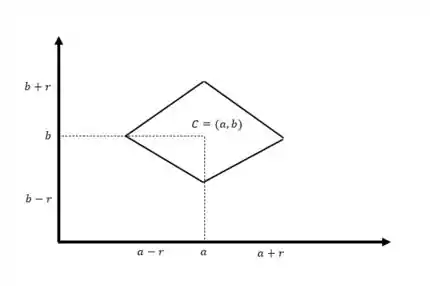
Prontinho! Essa deve ser a nossa bola centrada em quando definimos a norma como a soma no .
Resposta
Resposta no texto.